
Le gâteau d'anniversaire - Solution de l'énigme publié le 16/03/2012
Voir l’énoncé de l’énigme
Découpe du gâteau
- On choisit un point vers le centre du gâteau qui se trouve à moins de 17 cm des 4 sommets ; il est noté E sur la figure ci-dessous.
- On coupe le gâteau en partant de E jusqu’à chacun des 4 sommets.
- La première jumelle mangera les deux parts vertes AEB et CDE et la deuxième jumelle mangera les deux autres parts bleues BCE et ADE.
- Ce partage est équitable !
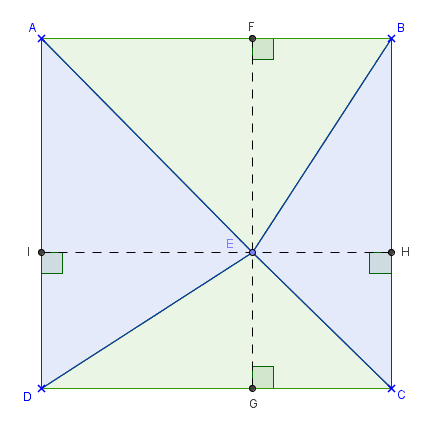
Justification de l’égalité des parts
- Imaginons que les droites parallèles aux côtés du carré qui passent par E soient tracées.
- La première coupe le côté [AB] en F et le côté [CD] en G.
- La deuxième coupe le côté [BC] en H et le côté [AD] en I.
- Les quadrilatères AFEI, BHEF, CGEH et DIEG sont des rectangles partagés en deux triangles rectangles de mêmes aires par l’une de leurs diagonales.
- Aire(ABE) + Aire(CDE) = Aire(AEF) + Aire(BEF) + Aire(CEG) + Aire(DEG)
- Aire(ABE) + Aire(CDE) = Aire(AEI) + Aire(BEH) + Aire(CEH) + Aire(DEI)
- Aire(ABE) + Aire(CDE) = Aire(AEI) + Aire(DEI) + Aire(BEH) + Aire(CEH)
- Aire(ABE) + Aire(CDE) = Aire(ADE) + Aire(BCE)

