Un exemple d'œuvre travaillée en classe de mathématiques publié le 16/03/2012  - mis à jour le 21/06/2017

Une histoire de formats

D’abord $\sqrt{2}$

Le chapitre sur les racines carrées a mis l’accent sur l’existence de nombres un peu particuliers, les nombres irrationnels. Après une approche historique du nombre $\sqrt{2}$, obtenu comme la longueur de la diagonale d’un carré de côté 1 unité, nous avons démontré en classe que ce nombre n’était pas décimal puis qu’il n’était pas non plus rationnel.
Nous avons ensuite poursuivi l’étude de ce fascinant nombre $\sqrt{2}$ en nous intéressant aux formats de rectangles. Nous nous sommes appuyés sur les formats de papier : A4, A3,... Nous passons du format A3 au format A4, en pliant des feuilles A3 en deux, puis du format A4 au format A5 en pliant également en deux une feuille A4.
L’exigence du format normalisé A est que les feuilles successives gardent le même "aspect", ce qui se traduit mathématiquement par la conservation du rapport $\frac{\mbox{longueur}}{\mbox{largeur}}$. Sous ces conditions, en partant d’une feuille $A_{n}$ de format $L\times \ell$, que nous plions en deux, la nouvelle feuille est au format $\ell\times \frac{L}{2}$ :

La conservation du rapport mène alors à l’équation :

$$\frac{L}{\ell}=\frac{\ell}{\frac{L}{2}}$$

soit :

$$\left(\frac{L}{\ell}\right)^2=2$$

Le nombre $\sqrt{2}$ apparaît alors comme la seule réponse de proportion conservant le format par pliage en deux.

Puis le nombre d’or $\Phi=\frac{1+\sqrt{5}}{2}$

On étudie ensuite un autre exemple de format de rectangle :
le rectangle d’or dont les proportions vérifient la définition suivante :
Un rectangle d’or est un rectangle dont les dimensions $L\times\ell$ sont telles que si on lui retire le carré formé sur sa largeur, le rectangle restant de dimensions $\ell\times(L-\ell)$ a le même rapport que le rectangle de départ.

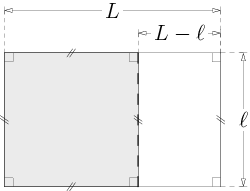
La conservation du rapport se traduit cette fois-ci par l’équation :

$$\frac{L}{\ell}=\frac{\ell}{L-\ell}$$

et qui donne l’équation du second degré :

$$\left(\frac{L}{\ell}\right)^2-\frac{L}{\ell}-1=0$$

Le nombre $\Phi=\frac{1+\sqrt{5}}{2}$, unique solution positive de cette équation est défini comme le nombre d’or.

 

 Page suivante : Le nombre d’or en peinture