
Présentation des TraAms 2019-2021 publié le 15/12/2019 - mis à jour le 05/05/2021
La compétence Modéliser
Sommaire des TraAms "modéliser"
L’approche par compétences apparait dans les programmes au début des années 2000 avec notamment le socle commun des connaissances et des compétences paru en juillet 2006.
Cette approche marque un changement de paradigme. Elle tend à bouleverser la répartition des rôles "enseignant/élève". Elle n’engage plus les enseignants vers une transmission de savoirs académiques mais vers une construction de situations accompagnées de problématiques dans lesquelles, les élèves vont devoir découvrir les savoirs et se les approprier pour y répondre. Cette approche place donc l’élève au centre de l’apprentissage et le rend responsable de construire lui-même ses propres connaissances. L’enseignant se retrouve donc "facilitateur" de cette construction en lui mettant à disposition des "instruments".
La compétence MODÉLISER traverse les programmes de Mathématiques.
Ce document donne la description de la compétence Modéliser dans les programmes à travers les niveaux du cycle 2 au Lycée.
Cette compétence s’associe pleinement à la notion de culture mathématique décrite dans les résultats de l’enquête PISA 2015.
La culture mathématique est l’aptitude d’un individu à identifier et à comprendre le rôle que les mathématiques jouent dans le monde, à produire des jugements fondés impliquant les mathématiques, et à s’engager dans des activités mathématiques, en fonction des exigences de sa vie en tant que citoyen constructif, impliqué et réfléchi.
Le rapport Villani-Torossian réaffirme la place de cette compétence. Elle est nécessaire dans de nombreux domaines tels que la santé, l’économie, la conception graphique et constitue une source intéressante de démarche de projet, vecteur de motivation chez les élèves.
Elle souligne l’importance d’utiliser les mathématiques pour résoudre des problèmes issus de la vie quotidienne, pour traduire une situation réelle.
Pour cela, le professeur est invité à faire utiliser le concept de proportionnalité et plus tard la batterie de fonctions pour établir la dépendance entre deux quantités. Cette approche par compétences conduit l’enseignant à questionner l’apprentissage des Mathématiques : dans quelles situations peut-on inscrire les élèves dans cette démarche ? La contextualisation est porteuse de sens : comment construire une situation vecteur d’explication facilitant les acquisitions des élèves ?
On peut réfléchir alors, par exemple, à la nécessité d’étudier la géométrie. En interrogeant, les élèves à l’entrée au Lycée, on constate souvent qu’ils se sont peu questionnés sur le sujet. Ils ont bien intégré qu’elle est nécessaire en architecture mais peu sont capables de faire le lien avec le secteur automobile, les images de synthèse, les œuvres d’art, ... qui constituent de nombreuses situations à étudier comme, par exemple, la fresque "L’École d’Athènes" du peintre italien Raphaël.

L’École d’Athènes du peintre italien Raphaël.

Le découpage du tableau avec certaines lignes géométriques
Voici un diaporama qui illustre l’intérêt et les applications de l’étude de la géométrie.
Diaporama réalisé par D.Gaud dans le cadre de l’IREM. Il peut accompagner un échange avec les élèves sur l’intérêt d’étudier la géométrie.
« Les sciences n’essayent pas d’expliquer, c’est tout juste si elles tentent d’interpréter, elles font essentiellement des modèles. Par modèle, on entend une construction mathématique qui, à l’aide de certaines interprétations verbales, décrit les phénomènes observés. La justification d’une telle construction mathématique réside uniquement et précisément dans le fait qu’elle est censée fonctionner ». John Von Neumann
Les probabilités sont aussi un secteur privilégié pour travailler la modélisation. Le programme de première de 2001 a réalisé une avancée importante pour appuyer l’intérêt de modéliser dans l’enseignement secondaire. L’arbre de dénombrement ou de probabilité constitue bien souvent la modélisation recherchée et les diverses manières de l’obtenir dynamise les élèves. Le passage du discret au continu reste aussi l’objectif à atteindre dans de nombreux domaines.
La simulation numérique est plébiscitée à partir du cycle 4. Il convient de proposer des situations intégrant l’utilisation de logiciels tels que le tableur et les langages de programmation Scratch et Python. Cela s’intègre pleinement dans la volonté des programmes qui demande de valider ou invalider le modèle choisi.
Plus largement, cette compétence est relancée dans les nouveaux programmes de 2019 du Lycée. En effet, dans l’enseignement scientifique proposé en première, elle fait partie intégrante de la démarche scientifique qui rayonne notamment en sciences physiques.
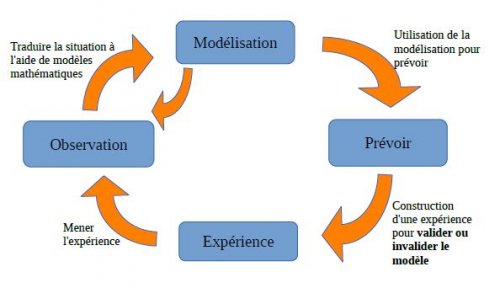
Ce schéma propose la démarche scientifique intégrant pleinement la modélisation.
Il semble donc intéressant de mettre en évidence les représentations des élèves sur l’observation des situations de la vie courante comme par exemple le soleil.
Cependant, on constate que les situations les plus intéressantes sont souvent complexes ainsi que les outils mathématiques mis en jeu. On peut s’en rendre compte aisément ici :
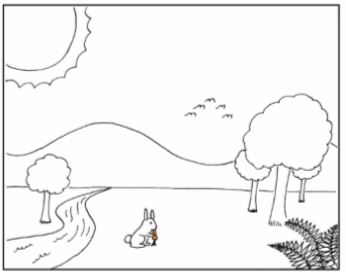
Image illustrant les différentes modélisation possibles à l’observant d’une simple scène.
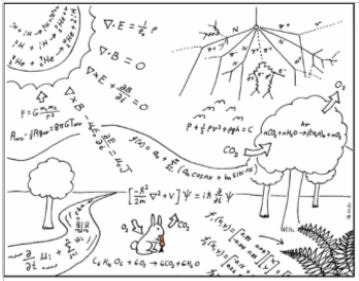
Image illustrant les différentes modélisation possibles à l’observation d’une simple scène.
On peut donc s’interroger sur la manière dont les élèves découvrent la modélisation pour à la fois trouver une situation exigeante et proche des capacités des élèves, mais aussi, des savoirs attendus dans les programmes. Elle doit être le déclencheur de l’intérêt et de la motivation. Être attractive pour permettre à l’apprenant, spontanément, de vouloir s’engager dans la démarche. Cela relance aussi le temps consacré en classe dans les tâches à prise d’initiatives.
- Comment se construire des points de repères en tant qu’enseignant pour construire une tâche de modélisation ?
- Comment mener la tâche de modélisation avec les élèves ? ( Le temps, la phase anticipée, la phase transmissible, l’institutionnalisation, la trace écrite, l’organisation matérielle, la structuration de la classe... )
- Quel est la nature, l’objectif de la tâche de modélisation ? ( Utiliser, critiquer, créer le support de la modélisation )
- Comment impliquer/motiver les élèves dans la tâche de modélisation ?

