TraAM 2017-18 : Comment ça "fonctionne" ? publié le 24/05/2018 - mis à jour le 05/04/2019
Caractéristiques du scénario
Thématique
Introduction aux fonctions mathématiques avec scratch. (scratch est seulement utilisé, pas de programmation, celle-ci est déjà faite, c’est juste de la lecture de scripts tout au plus)
Niveau concerné
Fin de cycle 4.
Compétences mobilisées
Chercher, raisonner et communiquer.
Problématique
Le programme scratch demande un nombre. Il faut essayer de deviner celui qui va être renvoyé et pour cela répondre à la question : Quelles sont les procédés qui ont permis de passer du nombre donné au nombre renvoyé ?
Nombre d’heures envisagées
Environ 2 × 1 h
Une séance avec les fichiers Scratch.
Une séance dans des conditions “classiques”.
Outils et ressources
On a besoin des 9 fichiers Scratch ci-dessous et de quoi les utiliser (salle informatique, tablettes…)
Les élèves ont besoin de leur cahier pour marquer leurs observations mais on peut aussi utiliser en plus un outil comme SOCRATIVE (lien vers l’article SOCRATIVE) pour récupérer les réponses numériquement et en faciliter l’exploitation. Voici un “quiz” SOCRATIVE tout près par exemple que vous pouvez importer dans votre espace enseignant SOCRATIVE (si vous en avez un) :
https://b.socrative.com/teacher/#import-quiz/34515915
L’identifiant du quiz est : SOC-34515915
Déroulement du scénario
Très important ! Ne pas parler de fonction mathématique avant la fin de la séance 1. L’objectif est qu’ils cherchent des fonctions mathématiques sans s’en rendre compte et après seulement, qu’ils mettent un nom dessus.
Séance 1 :
L’activité est basée un peu sur le principe d’une boite noire dont on cherche à trouver le fonctionnement : un nombre est donné, un autre nous est renvoyé, il faut trouver comment le nombre correspondant est obtenu. Pour cela, l’élève donne un nombre. Il fait ensuite une proposition. Si ce n’est pas le nombre attendu alors on lui dit ce qu’il aurait du répondre.
La première partie peut se faire individuellement ou à deux. Être à deux peut être un plus car les échanges peuvent être très intéressants.
La consigne est la suivante : ils ont 9 fichiers Scratch.
Voici le premier :
Ils les ouvrent dans l’ordre et à chaque fois, reportent sur leur cahier ce qu’on leur demande de la façon qu’ils veulent : langage français, mathématique, un mélange...
Sur les neuf fichiers, il y en a huit qui correspondent à des fonctions affines et le dernier qui correspond à la fonction carré. Parmi les huit, deux sont des fonctions constantes et trois des fonctions linéaires. Dans l’ordre, cela donne : 2x ; 4 ; x+1 ; -2 ; -x ; 3x - 1 ; 1,5x ; -x+20 ; x².
Remarque : les élèves ont le choix concernant le nombre qu’ils donnent mais peu, voir aucun, suivant les classes, n’utilisent la stratégie de tester systématiquement un et zéro.
Il y a un dixième fichier nommé “4_a_creer.sb2” qui est prévu pour être utilisé de la manière suivante : les élèves les plus rapides peuvent créer eux-même leur fonction et la faire chercher par les autres. Un manque de temps n’a pas permis de tester cette possibilité.
Dans un fichier Scratch, tous les scripts sont accessibles, donc il a fallu masquer un peu la partie qui correspond à la fonction. Elle est dans la partie scripts de la scène. Les élèves commencent à assez bien savoir manipuler Scratch (en 2017) donc certains les trouvent. Encore faut-il qu’ils trouvent aussi les formules correspondantes puis qu’ils les réduisent. Elles ne sont pas lisibles directement :
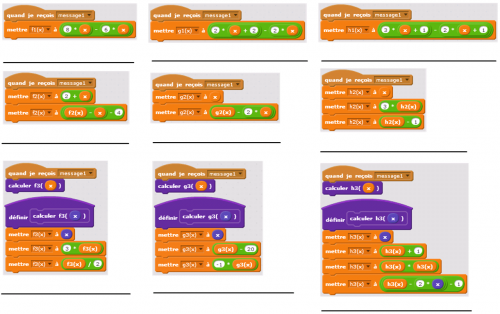
Pour les trois premières fonctions, l’expression informatique doit être transformée en expression mathématique, puis il faut effectuer une réduction assez simple.
Pour les trois suivantes, il faut suivre l’évolution d’une variable, trouver l’expression mathématique, puis la réduire.
Pour les trois dernières, il y a l’utilisation très artificielle d’une fonction informatique pour se rapprocher d’une fonction mathématique (un bloc violet) et de variables qui est un peu plus difficile à décoder. Il y a même un développement du type (a+b)² avant une réduction pour la neuvième.
Ces scripts peuvent être utilisés pour faire du calcul littéral sachant que les élèves connaissent la formule à trouver. Mais attention, à partir de la quatrième fonction, on peut vite perdre certains élèves. Dans tous les cas, ce travail n’est pas à faire à suivre, il faut le séparer de plusieurs séances avec cette première activité et il est à moduler en fonction du niveau de la classe.
On peut parler des fonctions informatiques de Scratch (les blocs violets), et de cette différence avec les fonctions mathématiques :
Une fonction mathématique, quand elle est utilisée, devient un calcul dont on récupère le résultat ;
Une fonction scratch, quand elle est utilisée correspond à une suite “d’actions” qui peuvent éventuellement dépendre de variables ce n’est pas un nombre. C’est “juste” un nom donné à un regroupement de blocs.
C’est bien différent de l’écriture mathématique f(x) qui correspond elle à un nombre. Par contre, les fonctions en langage Python peuvent correspondre à des fonctions mathématiques et être utilisée comme telles .
Pour l’introduction du vocabulaire, bien leur faire penser à ce qu’ils ont cherché durant cette activité, et surtout à ce qu’ils n’ont pas cherché : ils n’avaient pas à trouver des nombres mais à trouver les procédés permettant d’arriver aux nombres, comment cela fonctionnait, le fonctionnement, et en arriver à la notion de fonction mathématique.
Remarque : Pour certains, les temps d’affichage des dialogues peuvent être trop longs et freiner ainsi leurs recherches. C’est un peu le but pour qu’ils aient envie de chercher dans les scripts le moyen de les raccourcir.
Séance 2 : (qui peut se faire dans des conditions “classique”)
Quand on a validé les descriptions des neuf fonctions, on leur demande de les traduire en formule dans un premier temps, puis on leurs montre la façon de définir des fonctions avec la nouvelle flèche. Pour cela, on utilise les noms simplifiés suivants : pour le premier fichier avec Fany on utilisera comme nom de fonction f1, puis g1, h1 et f2, g2… On parle aussi d’antécédent et d’image.
On peut à ce point, soit enchainer directement, soit laisser passer plusieurs semaines avant d’aborder le cas particulier des fonctions linéaires et affines.
Une fois qu’elles sont définies avec la notation mathématique, on demande à chacun de faire des regroupements en choisissant des critères. Les deux fonctions constantes sont bien souvent les premières à être regroupées. En ce qui concerne les autres, les critères sont parfois surprenants et nous permettent de voir la représentation que les élèves ont des formules.
Pour guider un peu plus les regroupements (à moins que tous les groupes aient été trouvés), on fait remplir un tableau de ce type :

Note : Le remplissage du tableau demande une dizaine de minutes. Les plus rapides doivent généralement revoir minimum une ou deux lignes.
g3 peut poser des difficultés écrite dans ce sens : -x+20.
Les élèvent mettent aussi a=x pour h3 et c’est l’occasion de faire une distinction sur l’utilisation des lettres en mathématique.
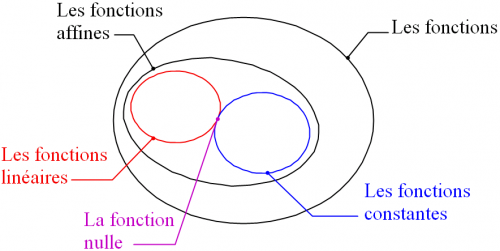
On peut ainsi montrer que toutes sauf la dernière peuvent être écrites sous la forme ax+b, celles ayant a=0 étant de plus constantes et celles ayant b=0 étant de plus linéaires.
Retours d’expérience
Séance 1 :
Le fait que les élèves puissent vérifier seuls leurs réponses est très pratique et permet à chacun d’avancer à son rythme.
Les fonctions constantes déstabilisent certains élèves et ils ont du mal à décrire leur fonctionnement. Pourtant, elles modélisent des situations de la vie courante comme les forfaits illimités par exemple… Elles permettent de faire le lien avec les fonctions affines : elles sont composées d’une fonction linéaire ”plus” d’une fonction constante.
La fonction opposée a aussi droit à des descriptions peu directes.
Pour 1,5x c’est souvent “Elle prend le nombre et lui ajoute sa moitié.” qui est trouvé. On peut revenir sur 1,5x = 1×x + 0,5x = 1×x + ½ x
Sinon, pour certains, il suffit juste de leur faire oraliser et de leur dire : “Ce que tu viens de me dire, c’est la réponse, il te suffit de l’écrire.”
Cette façon d’aborder les fonctions sans au début utiliser le mot, permet d’éviter les commentaires du type “On va faire les fonctions, il parait que c’est super dur.” et donc d’éviter de partir avec des élèves qui n’y comprennent rien d’avance et avec une attitude défaitiste. Le fait de leur dire “Les procédés que vous avez été capables de trouver durant la séance, et bien c’est cela que l’on appelle des fonctions.”
Séance 2 :
Le fait de leur donner le choix pour les critères de regroupement les amènent à se poser des questions sur les points communs et les différences entre des formules, des fonctions. Cela aide aussi à comprendre l’écriture ax+b.
Cela remontre à certains des multiplications cachées : x = 1 × x ; -x = -1 × x.
Conclusion :
C’est une activité où les élèves sont motivés et actifs. Elle peut servir de référence tout au long de l’année : “Vous savez, ce que vous avez fait avec Scratch...”. Et elle permet de bien mettre en place la notion de fonction.

