Découvrir l'intelligence artificielle à partir d'un jeu publié le 31/03/2022  - mis à jour le 16/06/2022

Arbre de jeu, approche probabiliste

Quelques semaines après cette introduction, lors d’une séance de deux heures, je suis revenu sur le jeu et j’ai sollicité leurs souvenirs pour reconstituer les règles du jeu. Abordant le problème de manière plus structurelle, je leur ai demandé au préalable combien de parties différentes il était possible de jouer. Les réponses ont été assez surprenantes : 3 , 6 (par rapport au nombre de pions), 5 (?), une infinité.

Nous avons ensuite construit ensemble les états de jeux des deux premiers tours : 3 possibilités pour les blancs au premier tour puis, pour chacune de ces possibilités, entre deux et quatre possibilités pour les noirs. Les élèves ont vite perçu la croissance "exponentielle" de l’arborescence : 3 états pour le premier tour, 10 états pour le deuxième, l’infinitude de l’arbre de jeu est dès lors apparue plus probable pour bon nombre d’élèves.

Je leur ai alors présenté la notion d’arbre de jeu qui permettait de dénombrer de manière rigoureuse le nombre de parties différentes, en insistant sur la représentation en arborescence, fondamentale en probabilités.

Arbre de jeu complet avant tronçonnage

La classe s’est alors constituée en 10 groupes de trois à quatre élèves et chaque groupe a reçu un tronçon de l’arbre de jeu, les tronçons étant déterminés par les dix états de jeu dénombrés à l’issue du deuxième tour. Il était alors demandé à chaque groupe de relever le nombre de parties contenues dans son tronçon ainsi que les victoires de chaque couleur puis de venir l’écrire au tableau.

• Hexapawn : arbre de jeu pour un début à gauche (OpenDocument Spreadsheet de 17.1 ko)

  Hexapawn : arbre de jeu pour un début à gauche

• Hexapawn : arbre de jeu pour un début à gauche (PDF de 40.6 ko)

  Hexapawn : arbre de jeu pour un début à gauche

• Hexapawn : arbre de jeu pour un début au centre (OpenDocument Spreadsheet de 19 ko)

  Hexapawn : arbre de jeu pour un début au centre

• Hexapawn : arbre de jeu pour un début au centre (PDF de 52.8 ko)

  Hexapawn : arbre de jeu pour un début au centre

• Hexapawn : arbre de jeu pour un début à droite (OpenDocument Spreadsheet de 16.5 ko)

  Hexapawn : arbre de jeu pour un début à droite

• Hexapawn : arbre de jeu pour un début à droite (PDF de 39.2 ko)

  Hexapawn : arbre de jeu pour un début à droite

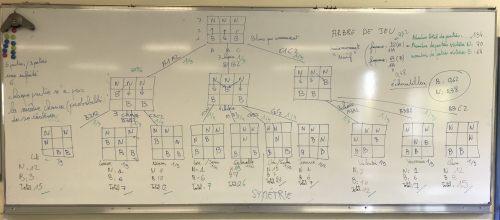
En quelques minutes, les valeurs demandées ont été écrites au tableau et les élèves ont spontanément remarqué la symétrie des effectifs selon un axe vertical. J’ai appuyé cette remarque en leur faisant aussi voir la symétrie des parties sur les états de jeux, avec un simple échange des colonnes A et C. La remarque sur la symétrie a été notée au tableau pour souligner l’importance de cette information dans la structure du jeu.

Dénombrement des parties

Collectivement, nous avons rapidement trouvé le nombre total de parties (134) ainsi que le nombre de victoires : 64/134 (48%) pour les blancs et 70/134 pour les noirs (52%), ce qui allait à l’encontre de la fréquence de l’échantillon statistique obtenu lors de la première séance. Comment expliquer une telle différence ? Aucun élève n’a osé proposé une explication et j’ai dû insister sur la notion de choix et commencer à mettre des "poids" sur les branches de l’arbre pour que les élèves suggèrent le mot "probabilités" comme mesure de la chance de réalisation d’une partie plutôt qu’une autre.
La détermination des probabilités d’un tour à l’autre n’a pas posé de problème mais la recherche de la probabilité d’une branche complète a donné lieu à des raisonnements erronés : le principe additif a été évoqué par une majorité d’entre eux et il a fallu faire le calcul de plusieurs branches pour montrer l’inexactitude du raisonnement.

Ayant déjà introduit la notion d’arbre de proportion pour les proportions échelonnées, j’ai invoqué leurs récents souvenirs du chapitre sur l’information chiffrée et leur ai proposé de considérer chaque branche comme une proportion échelonnée. Avec cette approche, le principe multiplicatif a été mis en évidence et a permis de valider les calculs des probabilités jusqu’au deuxième tour.

Afin de lever le dilemme sur l’équitabilité du jeu, je leur ai demandé de calculer la probabilité de chaque partie apparaissant dans leur tronçon et d’additionner les probabilités de chaque couleur.
Cette consigne demandait de la rigueur et sollicitait leur capacité à exploiter une représentation graphique en arbre afin de réaliser les produits des probabilités rencontrées le long de chaque branche, ces produits étant constitués de 3 à 7 facteurs. Par ailleurs, les groupes n’avaient pas la même charge de travail car le nombre de parties variait fortement d’un tronçon à l’autre (de 7 à 26 parties). Toutefois, les plus malins ont pu remarquer que certaines parties voisines avaient les mêmes probabilités, ce qui limitait les calculs.
Je passais dans les groupes afin de les aider dans leurs démarches de lecture et d’annotation de l’arbre et vérifier la validité des premiers calculs.
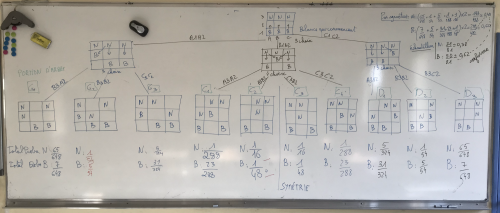
Comme pour le nombre de parties, les groupes les plus rapides ont marqué leurs résultats au tableau et j’ai complété les groupes manquants, en m’appuyant une nouvelle fois sur la symétrie des probabilités.

Calcul des probabilités de victoire de chaque couleur

À la fin, la probabilité théorique de victoire de chaque couleur a pu être établie : 259/432 pour les blancs (≈ 60%) et 173/432 pour les noirs (≈ 40%). Nous avons pu constater la conformité de ce résultat avec les fréquences de l’échantillon.

Dès lors, la modélisation probabiliste nous a amené à la conclusion de l’avantage théorique des blancs, lors d’un jeu aléatoire, sans pour autant statuer sur la question initiale de l’existence d’une stratégie gagnante.

 Page suivante : "Fiche synoptique" ; "Narration d’expérience : vers l’apprentissage machine"