Le luminobellule 3D : Découverte d'un neurone artificiel publié le 01/04/2022  - mis à jour le 16/06/2022

Sommaire des TraAms "Intelligence Artificielle"

Thématique

Deep Learning : Fonctionnement d’un neurone artificiel

Niveau concerné

Groupe de spécialité Mathématiques en Terminale.
Peut s’adapter en enseignement scientifique en Terminale.

Problématique

Comment, à partir de données numériques, peut-on prédire la couleur d’un insecte ?

Il s’agit ici de faire fonctionner en débranché puis sur machine un algorithme permettant de classer en deux groupes d’individus une population d’insectes à partir de trois entrées numériques et d’un résultat binaire (rouge ou bleu).

Les données de chacun des 40 insectes sont référencées sur des cartes de couleurs (20 rouges, 20 bleues).

De quelle couleur devrait être la carte noire ?

Contenus

La géométrie repérée dans l’espace, équations cartésiennes de plans dans l’espace, programmation en Python, listes.

Objectif

Voici ce que je souhaite faire émerger et expliquer aux élèves à la fin du traitement des données sur machine.

Graphiquement, on cherche les coefficients (les poids W1, W2, W3 et b) d’une équation cartésienne de plan séparant deux ensembles de points dans l’espace. L’algorithme mis en place permet, au fur et à mesure des erreurs de prédiction commises (entraînement), d’ajuster pas à pas les valeurs des poids (rétro-propagation).

Voici en images les points de l’espace (correspondants aux cartes rouges ou bleues) ainsi que les plans d’équations :

$$W_1X + W_2Y + W_3Z + b = 0$$

Situation de départ : poids = [5, 3, 1, -15]

Exemple d’état après un entraînement du modèle sur 20 cartes : poids = [2.9, 1.5, -0.1, -15.6]

Une vidéo contenant de belles animations pour expliquer le principe :

Remarques :

• On ne parlera pas de vectorisation ni de matrices ici afin de limiter la complexité.
• Je ne pense pas expliquer aux élèves le calcul de l’ajustement des poids mais cela reste possible en s’intéressant uniquement à un seul poids et en fixant les autres (minimisation par les moindres carrés). On peut donc penser à une activité présentant la recherche pas à pas du minimum sur une parabole convexe en utilisant les coefficients directeurs de tangentes. Cela pourrait permettre une rapide explication des calculs d’ajustements.

Un proposition de programme Python avec une animation 3D du résultat :

 Version exécutable en ligne avec FireFox ou Chrome (pyodide)

Nombre d’heures utilisées

2 heures. Après essai, je pense qu’une demie heure supplémentaire est nécessaire pour la présentation du diaporama de synthèse sur l’IA.

Outils et ressources

• Un jeu de cartes : Les données
• Une représentation schématique de l’algorithme sur feuille A4 plastifiée pour aider les élèves au départ.
• Des feutres pour tableau blanc effaçables
• Des chiffons
• Calculatrices
• Un environnement de programmation Python. (Capytale dans l’ENT)

Tous les documents pdf :

Démarche de l’enseignant

En observant les données présentées sur des cartes de couleurs, les élèves peuvent penser aux calculs de moyennes, de médianes et peut-être les associer à des points repérés dans l’espace.

Le fonctionnement, même simplifié, d’un neurone artificiel pour classer des données ayant peu de chance d’être apporté par les élèves eux-mêmes, j’ai choisi ici d’imposer une succession de calculs sur les données sans parler d’IA ou d’algorithme.

J’espère alors que les mots : "Algorithme", "Amélioration", "Apprentissage" voire "Intelligence artificielle" pourront être exprimés par au moins quelques groupes d’élèves au fur et à mesure de leur avancée dans la méthode proposée.

Une représentation dans l’espace du problème est donnée à la fin de la partie branchée pour faire le lien avec les équations cartésiennes de plans.

Déroulement du scénario

11 élèves seulement sont présents pour cette séance de 110 minutes en salle hybride (24 tables au milieu + 18 postes contre les murs). Nous venons de finir le thème sur l’orthogonalité dans l’espace et les équations cartésiennes de plans.

CK, une collègue de mathématiques du lycée, est présente avec nous à la fois par curiosité mais aussi pour analyser la séance. Merci !

t = 0 minute : Les élèves sont repartis comme d’habitude en îlots (4 ou 5 élèves par groupe). Le problème est présenté par la fiche "Introduction" :

Pour résumer, il y a 20 cartes bleues, 20 rouges et une noire. Sur chaque carte il y a 3 valeurs numériques. La question posée aux élèves est : "Quelle sera la couleur de la carte noire ?".

Ils ont à disposition les cartes de données et un temps est pris pour le débat et les idées. Des calculs de moyennes sont testés sans pouvoir réellement trancher.

t = 20 minutes : Je propose donc la mise en place d’un protocole avec distribution des rôles :

• Deux élèves pour les calculs
• Un élève pour noter sur la fiche plastifiée les valeurs données et calculées
• Un élève qui note sur son cahier l’évolution des valeurs des poids et tire au hasard les cartes

Les deux premières cartes traitées sont communes (voir le protocole). Cela permet aux élèves de comprendre ce qu’ils doivent faire.

Remarque : Pour ces deux cartes, j’ai pris une rouge puis une bleue, il faut peut-être inverser les deux pour ne pas commencer par une erreur nulle.

Les élèves tirent ensuite des cartes au hasard puis appliquent le protocole. Je passe dans les îlots pour réexpliquer ou m’assurer du bon déroulement.

Après quelques cartes traitées, les élèves observent de mauvaises prédictions sur les cartes bleues mais pas sur les cartes rouges (voir le graphique de la situation de départ).

Puis, en discutant avec eux, les élèves donnent des analyses du type : "IL fait encore des erreurs mais IL s’améliore, IL s’adapte, ... ".

Les élèves ont bien tête l’idée d’algorithme mais n’utilisent pas au début ce mot. Je dois leur demander : "Qui IL ?".

Au bout de 20-25 minutes, deux des trois îlots observent que l’algorithme offre de bonnes prédictions sur les 6 ou 7 dernières cartes, même sur les cartes bleues. Ces deux îlots ont déjà traité une vingtaine de cartes. Le troisième îlot est à la peine, une mauvaise organisation au départ. Je laisse donc encore 10 minutes de traitements.

Je demande aux deux îlots bien avancés de répondre à la question posée : Prédire la couleur du luminobellule capturé (la carte noire).

t = 55 minutes : Nous passons à la synthèse après qu’au moins 20 cartes aient pu être traitées par les trois îlots.

Ma question : Comment décrire ou analyser ce que vous venez de mettre en place ?

Les mots "Algorithme" et "Apprendre" sont utilisés puis, un élève parle d’"Intelligence artificielle". La classe semble accepter, en silence, cette idée et je suis bien en retard sur le déroulement prévu.

t = 65 minutes : Présentation/discussions autour de l’IA et du Deep Learning à l’aide du diaporama de support.

N’ayant que la moitié de la classe et manquant de temps, c’est cette phase qui aurait dû être reportée ultérieurement afin de laisser plus de temps aux élèves sur machine.

Vers la fin de la présentation, j’écris au tableau : $$w_1\times C + w_2\times A + w_3\times P + b > 0$$

"A quoi cela vous fait-il penser ?

Il faut quelques secondes avant qu’une élève parle d’équation de plan et associe les cartes à des points repérés dans l’espace. A l’aide matplotlib, j’affiche un exemple de représentation graphique du travail effectué.

A l’aide du schéma d’un neurone artificiel, je parle de la fonction d’activation. Ici nous avons utilisé une marche (0 si le résultat du calcul est négatif et 1 sinon) :

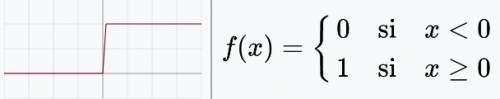
En demandant : Quel est le "problème" avec cette fonction ?, les élèves parlent de discontinuité et de non dérivabilité en 0.

Comment pourrions-nous rendre plus "régulière, lisse, smooth" cette fonction ?, certains élèves font le rapprochement avec le dernier DM sur la fonction sigmoïde.

J’aurai aimé prendre plus temps ici, demander aux îlots les poids trouvés à la fin et afficher les plans, parler de cette fonction sigmoïde permettant de prédire la couleur d’une carte de façon probabiliste. Un lien avec la fonction Log Loss pourrait être fait.

t = 85 minutes : Une question du style : "Imaginons que nous n’ayons pas 40 cartes à analyser mais 1000. Que pourrions-nous faire ?"

Une fiche est distribuée aux élèves afin de compléter ensemble le programme Python avant le passage sur machine.
Je prends rapidement le temps de réexpliquer l’utilisation des listes en Python avant de compléter le code avec eux. La classe a été assez efficace.

Il reste à peine 10 minutes pour se connecter aux ordinateurs, à l’ENT et compléter le notebook Python. Une seule élève a eu le temps de programmer l’algorithme en entier.

Réussites, obstacles et limites

Retour sur l’objectif initial :

Mon but premier était de "démystifier" l’IA et l’apprentissage machine en faisant le lien avec certaines notions mathématiques et algorithmique parcourues par les élèves cette année. Ce but est, me semble-t-il, atteint. Durant ces deux heures, les élèves n’ont pas vraiment travaillé ces notions mathématiques. Peut-être davantage la partie algorithmique. Le devoir à la maison sur la sigmoïde (qu’il faut réagencer car trop haché) peut permettre un travail plus approfondi autour des notions mathématiques. Un temps supplémentaire aurait pu être pris pour renforcer le lien entre le fonctionnement de ce neurone artificiel et cette fonction sigmoïde.

Modifier le découpage du temps :

Comme dit dans le déroulement, la phase de présentation du diaporama et les discussions associées a pris trop de temps et il aurait été souhaitable de reporter cette phase sur une autre séance.
On peut aussi introduire l’activité 20 minutes avant la fin d’une séance, discuter des idées (calculs de moyennes...) et poursuivre le travail au cours suivant...

Une phase de calculs un peu longue :

Il faut entre 15 et 30 minutes aux îlots pour commencer à obtenir de "bons" poids dans la partie débranchée. Cela peut être long notamment pour un îlot qui ne s’organise pas très bien. En classe de seconde (même activité en deux dimensions), après une dizaine de cartes traitées, certains groupes d’élèves très organisés ont effectué les calculs sur deux cartes en même temps. Ils ont pu ainsi balayer les 40 cartes en 25 minutes. Deux groupes d’élèves ont "choisi", après quelques minutes, de traiter 4 ou 5 cartes bleues pour "faire bouger les poids". Il y a là peut-être des idées à creuser pour rendre cette phase moins fastidieuse.

Les plateaux plastifiés servent surtout pour les premiers tours de calculs. Ensuite, les groupes les plus organisés s’appuient sur les deux élèves ayant une calculatrice et la mémoire qui note/donne l’état des poids. Je m’interroge donc sur la nécessité de ces plateaux, il faudrait peut-être les faire autrement.

J’ai choisi de ne pas parler d’IA avant de présenter le protocole à effectuer. En effet, je souhaitais que cette idée "d’algorithme qui apprend" vienne des élèves. Ce type d’algorithme ayant peu de chance de venir des élèves eux-mêmes, faut-il leur dire qu’ils vont faire fonctionner une IA avant de les lancer sur les calculs et ainsi espérer une plus grande adhésion ?

Recherche du jeu de données :

Ces données imaginaires m’ont permis d’ajuster les valeurs des 40 cartes afin d’observer, après un nombre limité de calculs, une évolution du modèle. Il existe des jeux de données réelles mais je préférais pouvoir modifier les données.

Prolongements

Autre type d’apprentissage : Hexapawn

Après quelques semaines et avec une classe entière cette fois-ci, j’ai envoyé les élèves tester un jeu en ligne pendant 20 minutes :

 Hexapawn : jeu en ligne

Leur mission : Effectuer au moins 15 parties, trouver les règles du jeu et analyser ce qui passe.

Quelques bugs sont découverts par les élèves mais ils ont tous compris cette idée d’apprentissage par renforcement.

Ajustement des poids :

On peut aussi penser à une activité présentant un algorithme de recherche pas à pas du minimum sur une parabole convexe en utilisant les coefficients directeurs de tangentes. Cela pourrait offrir une première explication des calculs d’ajustements.