Livraison par un drone publié le 26/03/2021 - mis à jour le 08/05/2021
Modéliser le déplacement d'un drone
Sommaire des TraAms "modéliser"
Description de la tâche de modélisation
Problématique
Le futur dans lequel les drones livreront à notre porte les commandes passées sur internet est devenu présent. Ces objets volants connectés se multiplient, se démocratisent et sont devenus accessibles. Leurs fonctionnalités sont aujourd’hui programmables avec des logiciels abordables pour des élèves.
Il était donc intéressant de les exploiter comme source de motivation et comme support dans une séquence de modélisation.
Les "petits" drones pouvant voler en intérieur sont dépourvus de géolocalisation pour pouvoir se repérer dans l’espace. Déplacer ce type de drone à un endroit précis en donnant des coordonnées devient alors un véritable défi pour les élèves.
Niveau concerné
Classe de 3ème
Modèles mathématiques utilisés
Proportionnalité, repère et coordonnées
Autres compétences mathématiques mise en jeu
Représenter, Calculer, Chercher
Compétences numériques
Programmation
Nombre d’heures envisagées
Deux séances de deux heures
Démarche de l’enseignant
La programmation par blocs fait partie du programme du cycle 4 de mathématiques. En plus, des séances dites "classiques" de programmation avec scratch (programme de calcul littéral, programme de construction, etc ...), utiliser un objet connecté peut aider à donner du sens.
L’idée est donc d’utiliser un drone afin de livrer un objet à un endroit choisi par l’exécuteur du programme.
Problématique rencontrée : il n’est pas possible d’utiliser des blocs "avancer" d’une distance donnée comme pour un lutin lors d’une construction géométrique par exemple. Le challenge proposé aux élèves est donc de pouvoir envoyer un drone sur une cible bien définie sans utiliser ces blocs de déplacement.
On peut penser que l’introduction d’un repère semble être une voie à exploiter.
Outils utilisés
Le drone : Parrot mambo

Les élèves du collège sont équipés de tablette, on utilise donc une application de programmation.
Application : Tynker

Le drone se connecte en Bluetooth à l’application Tynker
Description du déroulement de la séance
Première étape : Découverte et réflexion
Présentation du projet livraison par un drone aux élèves.
Mission : vous devez créer un programme permettant au drone de livrer un colis à un endroit précis donné par le client. Pour cela, vous disposez de l’application Tynker et d’un drone.
Ainsi, pour commencer, on fait réfléchir les élèves en groupe à cette problématique.
Les élèves se rendent compte de la difficulté d’associer le déplacement du drone et sa position dans l’espace puisque il n’est pas possible de dire au drone d’avancer par exemple d’un mètre.
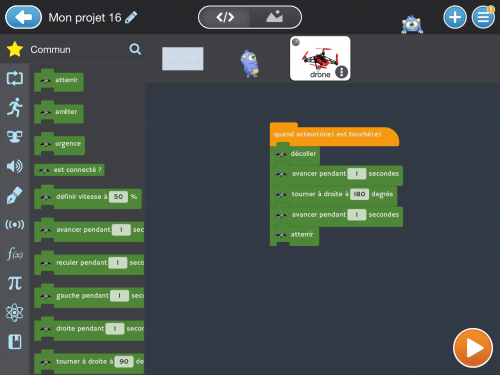
Blocs possibles pour le drone :
On constate que le drone se déplace un temps défini et avec une vitesse notée en pourcentage ce qui rend le positionnement difficile à modéliser dans un premier temps, en tous les cas non direct.
Deuxième étape : Tester, mesurer.
Les élèves testent le rapport vitesse en pourcentage, durée et distance parcourue.
Mise en œuvre : Chaque groupe dispose d’un drone et doit faire des mesures avec un mètre dans le couloir et la salle, des distances parcourues en fonction de la vitesse en pourcentage et de la durée du déplacement.
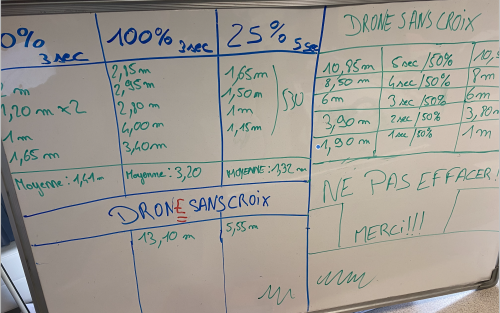
Objectif : faire un choix du pourcentage de vitesse pour associer une durée et une distance.
Après de multiples essais, les élèves ont pu se rendre compte que les drones n’avaient pas tous les mêmes réglages d’usine. La conclusion a été rapidement unanime, le plus simple était de régler le pourcentage pour obtenir un déplacement d’1 mètre en 1 seconde. Certains drones auront ainsi un réglage de la vitesse à 50% quand d’autres seront à 100%.
A travers, cette réflexion, les élèves ont exploité la notion de proportionnalité pour leurs calculs mais ont surtout dû faire des essais, et des choix pour parvenir à un modèle mathématique adapté à leur futur programme.
Des réglages de vitesse au déplacement dans l’espace
Une fois la vitesse réglée et de ce fait la distance de déplacement (même si déplacement n’est pas toujours exact en fonction des perturbations d’air qu’il peut y avoir), les élèves ont du s’attaquer à la problématique du repérage. L’objectif étant de donner une position de livraison, le point cible doit être repéré par des coordonnées.
Un travail de modélisation de l’espace salle a été mis en œuvre. Comment déplacer le drone non plus dans un espace quelconque mais désormais dans un repère ?
La problématique de la séance suivante était de créer un repère virtuel, d’associer la position du drone à des coordonnées et surtout de livrer au point de coordonnées préalablement données.
Sur les premiers schémas des élèves, j’ai pu m’apercevoir de la difficulté à modéliser la position du drone dans la classe et de la faire évoluer jusqu’au point voulu.
Plusieurs problèmes apparaissent :
- le déplacement se caractérise par la variation des coordonnées.
- trajectoire du drone : ligne (direction ?), courbe
Les élèves et la modélisation
Différentes approches et différentes options
Un élève souhaitait se rendre directement en ligne droite vers la position et s’est rendu compte qu’il avait besoin de la distance de l’origine au point. Nous avons ainsi pu exploiter le théorème de Pythagore, notion plutôt bien comprise et souvent utilisée dans des problèmes concrets de calcul de longueur. La recherche de cette distance à parcourir est une nouvelle fois mobilisable facilement avec l’utilisation de la géométrie analytique.
Or, la distance qui semble envisageable à calculer pour un élève de collège n’est pas le seul paramètre à déterminer pour envoyer le drone à bon port.
Effectivement, reste le problème de l’angle. Cette notion a déjà été plus complexe à faire apparaître mais également à traiter. Les élèves n’avaient pas encore abordé la trigonométrie mais cette problématique a apporté une source de motivation à sa découverte. (Une idée pour une future introduction)
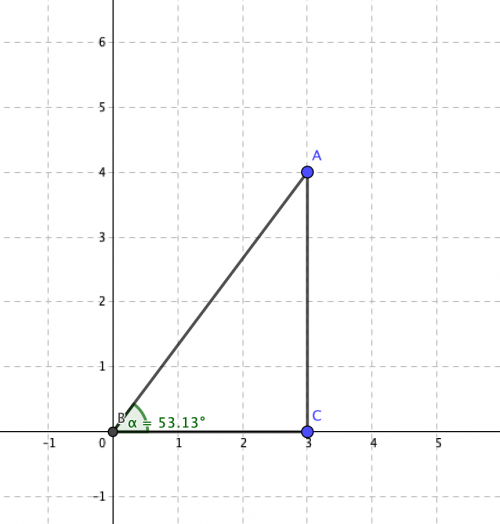
L’introduction et l’explication de la recherche de la mesure d’un angle à partir de la tangente n’ont été vues qu’avec un seul groupe qui a souhaité approfondir la solution du plus court chemin vers le point de livraison.
Les autres ont préféré des alternatives sur lesquelles nous reviendrons peu après.
Une fois l’angle déterminé à partir de l’abscisse et de l’ordonnée qui sont finalement devenus les côtés d’un triangle rectangle, le programme a pu commencer à être envisagé.
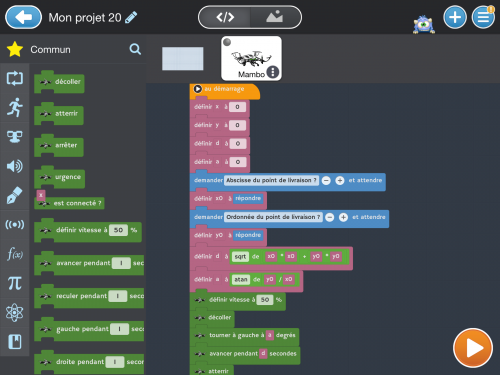
Plusieurs points importants : introduire une demande de coordonnées, utiliser des variables et les formules déterminées précédemment (calcul de la longueur et calcul de la mesure de l’angle).
Le programme a été finalement assez rapidement élaboré par le groupe car la difficulté reposait sur les calculs en fonction des coordonnées données. Quelques aides ont été apportées mais la quasi totalité a été réalisée en autonomie.
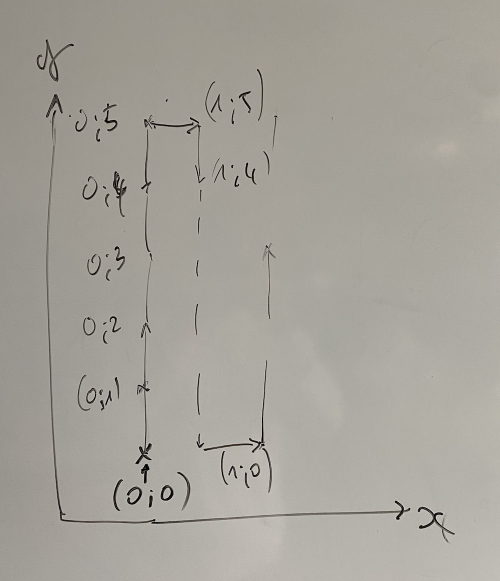
D’autres élèves ont fait le choix de déplacer le drone d’une manière algorithmique jusqu’au point de livraison. Ils souhaitaient faire évoluer les coordonnées du drone en fonction de son déplacement et le faire atterrir dès les coordonnées atteintes.
Les calculs sont dans ce cas plus simples et même inexistants. La difficulté demeure dans la programmation. Les élèves s’en sont vite rendus compte avec la mise en place de boucles "tant que", "jusqu’à ce que", de tests à chaque changement de coordonnées mais également à l’élaboration d’une clôture virtuelle. En effet, dans leur idée, le drone avance suivant y et à chaque seconde, donc à chaque mètre, y augmente de 1, mais du fait de leur quadrillage x doit augmenter de 1 au bout d’un moment et le drone doit alors revenir en arrière pour faire diminuer y de 1.
Bilan de ce choix : un programme long et complexe, un déplacement qui peut aussi être long en fonction des valeurs extrêmes choisies et des coordonnées du point de livraison.
Malgré tout, cette modélisation est intéressante sur le fait de quadriller un espace et de mathématiser un déplacement régulier et programmer dans un repère créé.
Un autre groupe a eu l’envie de faire déplacer le drone en spirale jusqu’au point de livraison. L’idée ressemblait à la précédente mais avec un déplacement moins couteux en distance et donc en temps. Ce groupe n’a pas pu aller au bout car la difficulté mathématique à laquelle il s’est heurté était trop grande. En effet, faire évoluer le rayon du cercle en fonction de la distance calculée avec le point de livraison s’est rapidement avéré trop complexe pour ces élèves. La démarche était néanmoins très intéressante.
Prolongement et perspectives
Le choix du déplacement direct vers le point pourrait être réinvesti en lycée en modélisant la situation par les coordonnées polaires.
Le choix de repérage du drone de manière circulaire peut être aussi à réfléchir avec l’équation du cercle.
Autre idée : utiliser l’optimisation de la distance d’un point à une droite, utilisation des vecteurs.