Comment modéliser un déplacement ? publié le 14/06/2020 - mis à jour le 09/04/2021
Sommaire des TraAms "modéliser"
Description de la tâche de modélisation
Problématique
L’étude des comportements est intimement liée à la notion de déplacements. Le déplacement d’un mobile est souvent difficile à reproduire en programmation. Quel modèle utiliser pour simuler un déplacement ?
Niveau concerné
Classe de Seconde
Modèles mathématiques utilisés
Vecteurs et équations de droite
Autres compétences mathématiques mises en jeu
Chercher
Compétences numériques
Création de contenu
Nombre d’heures envisagées
Deux séances de deux heures espacées d’exercices techniques sur les équations de droite.
Démarche de l’enseignant
La notion de vecteur est souvent difficile à contextualiser avec les élèves. La représentation du déplacement est souvent amenée en Physique-Chimie avec les forces.
Il est donc difficile de construire une situation permettant de faire comprendre l’intérêt de cette notion.
En navigation, il ressort que le bateau doit avancer pour savoir où il est. Cela est d’ailleurs un savoir-faire nécessaire pour obtenir son permis bateau : faire le point. Ce sont autant d’arguments permettant de justifier l’utilité de ce concept.
Plus largement, la question de modéliser un déplacement s’avère importante dans de nombreux domaines tels que la programmation de jeux vidéos. Mes recherches m’ont conduit sur la découverte de ce document (pdf de 512 Ko) présentant une modélisation des déplacements d’animaux dans l’étude de leur comportement.
J’ai donc exploité la page 4 pour proposer une tâche de modélisation.
La construction de cette tâche a pour but de faire émerger la notion de vecteur. Dans cet objectif, la formulation des questions a été réfléchie pour inviter les élèves à modéliser. Un déplacement en navigation est donnée par un cap et une vitesse. Afin d’atteindre la notion d’équations de droite et de coordonnées de vecteurs, j’ai volontairement choisi de les remplacer par un repère Ouest/Est et Sud/Nord. Les élèves risquent donc de bloquer simplement dans l’usage d’un repère pour pouvoir exploiter les consignes.
Description du déroulement de la séance
Pour commencer, j’ai présenté le document et les élèves ont compris les enjeux de ce travail. Ils se sont donc rapidement engagés dans la tâche. Le fait de considérer que l’animal est une biche a amusé les élèves et cela leur a permis de s’approprier la situation. La complexité de l’étude n’a pas bloqué les élèves dans leur motivation.
Une fois devant le document Geogebra, il a fallu largement accompagner les élèves vers l’apparition du repère.
Voici le document obtenu :
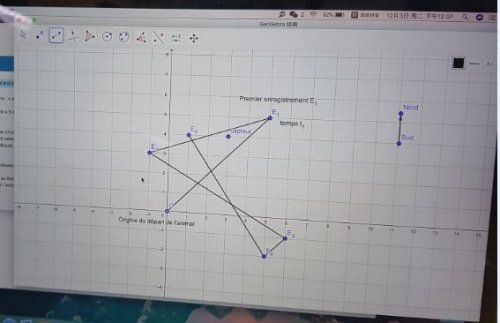
Cette photo présente le document geogebra produit par une élève après la construction du repère et le placement du capteur.
En revanche, une fois le repère ainsi construit, le placement du point représentant le capteur s’est fait aisément.
Les élèves ont alors déterminé l’équation de la droite. Les connaissances de troisième ont suffit à réactiver cette connaissance.
Voici la production d’un élève :
Production d’un élève pour déterminer l’équation de la droite du déplacement de l’animal
La synthèse a permis d’engager les élèves vers des exercices classiques sur la détermination d’équations de droites connaissant les coordonnées de deux points.
Voici le document Geogebra obtenu en fin d’étude :
Les élèves ont ensuite commencé le parcours de navigation :
Parcours navigation (HTML de 3.9 Mo)
Ce parcours sous forme de page internet amène les élèves vers la découverte de certaines notions en navigation et leur permet de faire émerger les représentations d’un déplacement.
L’aspect recherche de ce parcours a suscité enthousiasme et intérêt des élèves. Le passage par la construction d’un déplacement m’a permis de diriger les élèves vers la représentation mathématique d’un d’un vecteur.
Voici les productions de deux élèves :
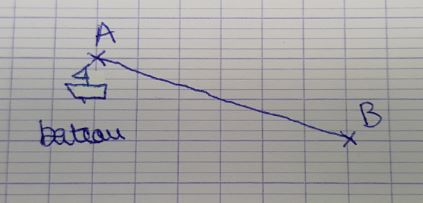
Représentation d’un élève pour modéliser le déplacement d’un bateau.
Représentation d’un élève pour modéliser le déplacement d’un bateau.
La situation île-bateau a permis plusieurs démarches. Une fois les élèves orientés vers la construction d’un repère, ils ont alors étudié avec soin les coordonnées possibles du bateau.
Deux démarches sont apparues chez les élèves, l’une centrée sur les équations de droites et l’autre centrée sur la somme de vecteurs.
Voici leurs productions :
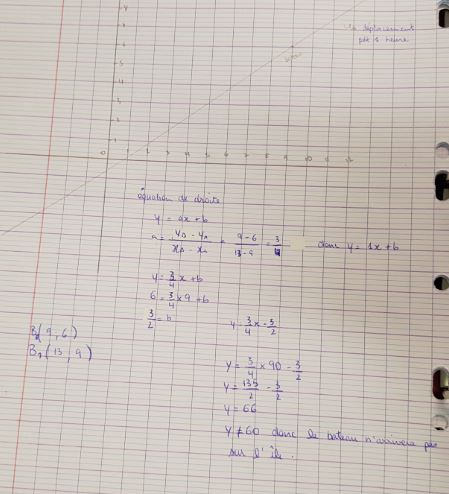
Production d’un élève utilisant les équations de droite pour montrer que le bateau n’arrive pas sur l’île.
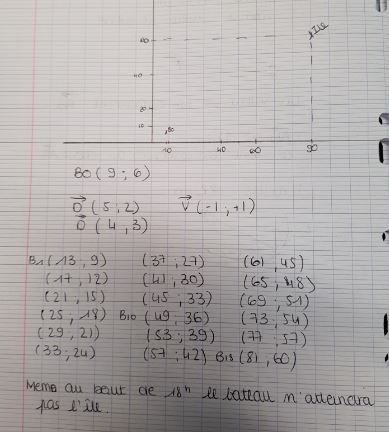
Production d’un élève utilisant les vecteurs pour montrer que le bateau n’arrive pas sur l’île.
Ces deux approches ont donné lieu à la confrontation des modèles.
Cette expérimentation a été menée par d’autres collègues. Voici d’autres productions d’élèves qui ont été mutualisées dans ce padlet :
L’utilisation du fichier Python illustre bien le contexte. Les élèves ont pu effectuer des tests pour observer les incidences sur le déplacement. Cette approche consolide la représentation d’un vecteur comme déplacement.
Certains ont alors procédé par tâtonnement pour trouver le mouvement du bateau à construire pour atteindre l’île.
La méthode experte est apparue : un élève a utilisé l’accroissement entre le bateau et l’île.
Voici sa production :
Production d’un élève pour déterminer le déplacement nécessaire pour atteindre l’île.
Le modèle construit en programmation Python a pu être critiqué par la méthode par tâtonnement. Certains élèves ont essayé (3,01 ;2,01) et cela a fonctionné car l’île est représenté par un carré. (voir Fichier structure du fichier déplacement bateau : structureF.py)
Les élèves et la modélisation
Dans le "parcours navigation", pour arriver à la représentation d’un vecteur par une flèche, il a fallu les accompagner avec ces questions : « Comment contrôle-t-on le sens ? », « Pourquoi ne mets-tu pas la flèche directement sur le déplacement ? ».
La construction d’un repère n’est pas acquise pour se représenter les conditions. Les élèves s’interrogent pour commencer : "Que faut-il faire ?", "Doit-on faire un autre graphique pour le vent ?". Ils ressentent des difficultés à modéliser les positions d’un mobile par des coordonnées de points. On peut s’interroger sur la présentation de cet attendu pourtant déjà présent au cycle 3.
Mis à part quelques élèves dont voici une production :
Production élève qui fait la somme de deux vecteurs en proposant une trajectoire du bateau non rectiligne.
La somme de deux vecteurs n’a pas constitué une difficulté. On peut néanmoins s’interroger sur la nécessité de préciser aux élèves que le bateau suit une trajectoire rectiligne. Il a aussi fallu pour certains donner le coup de pouce suivant : "Où sera le bateau au bout d’une heure ?" pour qu’ils commencent leur réflexion.
On observe ici l’expression des deux modèles : les équations de droite et les vecteurs. Cette expérimentation renforce le fait que les équations de droite sont liées à la notion d’alignement. Les élèves se dirigent naturellement vers cette notion pour montrer si l’animal passe par le capteur ou si le bateau passe par l’île. Le concept de vecteur devient nécessaire lorsque l’on ajoute deux déplacements. Le résultant des deux vecteurs ne peut se formaliser qu’à l’aide de la somme des deux vecteurs en ajoutant les coordonnées. Les échanges entre les deux modèles permettent d’illustrer l’intérêt des mathématiques pour étudier ce type de situations. Chaque élève a pu montrer ses tentatives de recherche et expliquer en quoi elles étaient plus ou moins pertinentes.
La simulation en langage Python facilite l’engagement des élèves dans la tâche. On peut regretter sur ce point qu’ils ne réalisent pas eux-mêmes le programme. Cependant, cela nécessite de bonnes compétences en programmation Python et n’apporte pas davantage dans la compréhension des deux modèles.
Prolongement et perspectives
Les élèves ont compris globalement l’intérêt de la modélisation. Le concept d’équation de droites semble acquis, son utilisation dans l’étude sur le bateau en témoigne. Il convient de rajouter qu’il s’en est suivi de nombreux exercices plus techniques accompagnés de vidéos explicatives :
Les vecteurs sous forme d’un déplacement ne demandent qu’à émerger auprès des élèves. Ils ont aussi été familiarisés en fin de cycle 4 avec la translation. (Compétence associée : "comprendre l’effet d’une translation, d’une symétrie (axiale et centrale), d’une rotation, d’une homothétie sur une figure")
Le jeu du casse brique proposé en fin de parcours illustre bien la modélisation. Les élèves ont bien compris l’idée du rebond de la balle sur les parois. On peut donc imaginer que les élèves s’emparent de cette problématique et réalisent le jeu dans d’autres circonstances.
Documents de référence
Parcours navigation (HTML de 3.9 Mo)
Ce parcours sous forme de page internet amène les élèves vers la découverte de certaines notions en navigation et leur permet de faire émerger les représentations d’un déplacement.
Déplacement bateau (Zip de 742 octets)
Fichier Python simulant le déplacement d’un bateau vers une île.
Fichier structure du fichier déplacement bateau (Zip de 594 octets)
Fichier structure lié au fichier déplacement bateau vers l’île. Il est placé dans le même dossier sinon le fichier "déplacement bateau" ne fonctionne pas.
Document professeur modéliser déplacement. (PDF de 280 ko)
Document professeur sur la modélisation d’un déplacement.
Document élève modéliser déplacement. (PDF de 246 ko)
Document élève sur la modélisation d’un déplacement.