Comment peut-on se représenter la Terre ? publié le 15/02/2020  - mis à jour le 09/04/2021

Sommaire des TraAms "modéliser"

Description de la tâche de modélisation

Problématique

L’histoire de la mesure du méridien terrestre par Ératosthène fait partie de l’histoire des représentations de l’homme du monde réel. Comment faire réagir les élèves sur l’évolution de ses représentations et surtout quel modèle peut permettre de déterminer les mesures attendues ?

Niveau concerné

Classe de Première en enseignement scientifique

Modèle(s) mathématiques utilisé(s)

Droites parallèles, angles alternes internes, proportionnalité

Autres compétences mathématiques mises en jeu

Chercher/Calculer

Compétences numériques

Communication et Collaboration

Nombre d’heures envisagées

Une séance d’une heure.

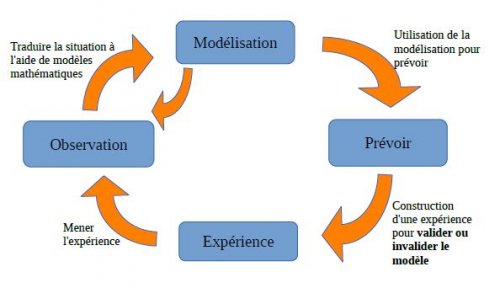
Démarche de l’enseignant

En première, la mise en place des nouveaux programme de 2019 de l’enseignement scientifique invitent naturellement à se poser la question de la place de la modélisation. Deux des objectifs majeurs sont :

• Comprendre la nature du savoir scientifique et ses méthodes d’élaboration.
• Identifier et mettre en œuvre des pratiques scientifiques : Valider/invalider un modèle.

Dans le thème La Terre, les élèves doivent savoir calculer la longueur du méridien terrestre par la méthode d’Ératosthène.
Nicolas DECAMP et Cécile de HOSSON, maitre de conférence en didactique à l’université Paris-Diderot, ont déjà réfléchi en 2011 à cette question :

Quelques éléments historiques et didactiques surl’expérience d’Ératosthène (PDF de 826.5 ko)

Bulletin de l’Union des Physiciens (1907-2003), Union des physiciens, 2011. hal-01663442 - Nicolas Décamp, C. de Hosson.

Il précise l’erreur d’une modélisation spontanée qui amène à représenter le soleil comme un point, voire comme un cercle, plus petit que la Terre d’où partirait les rayons lumineux.
J’ai donc voulu mesurer les représentations de mes élèves à travers cet enseignement.

Description du déroulement de la séance

Au préalable, j’ai fait réagir les élèves sur les théories des "platistes" qui remettent ainsi en cause des fait établis depuis des siècles. Cela a soulevé de vives réactions amusées chez mes élèves. Ils ont cependant rencontré des difficultés pour justifier que la Terre est ronde par des observations simples.

Padlet : la terre peut-elle être plate ? (PDF de 5.4 Mo)

Padlet présentant les argumentaires des élèves pour montrer que la Terre n’est pas plate.

Une fois cette controverse établie, je voulais qu’ils modélisent l’ombre du soleil sur la terre sans travailler tout d’abord sur le texte de Cléomède rapportant la démarche d’Ératosthène.
J’ai donc présenté succinctement la démarche d’Ératosthène : Il a ainsi utilisé deux gnomons en bois, l’un placé Syène, l’autre à Alexandrie, deux villes situées sur le même méridien, à une distance de 5000 stades (788 km) sur la Terre. Au solstice d’été, lorsque le soleil est au milieu du ciel, il se situe exactement à la verticale de Syène et le gnomons de Syène n’a pas d’ombre : le rayon solaire passe par le centre de la Terre.
Et, je leur ai demandé de modéliser la situation à l’aide d’un schéma : le soleil, l’ombre, les gnomons et la Terre.
Voici quelques représentations d’élèves :

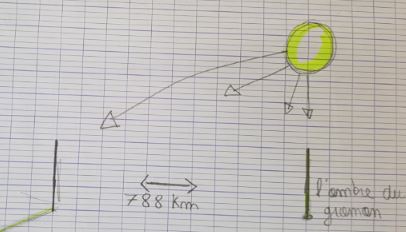
Représentation d’un élève présentant les
rayons du soleil et l’ombre obtenue sur un gnomon.

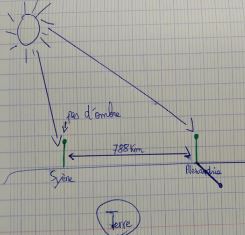
Représentation d’un élève présentant les
rayons du soleil et l’ombre obtenue sur un gnomon.

Certaines représentations ont été cependant très précises :

Représentation d’un élève présentant les rayons du soleil
et l’ombre obtenue sur un gnomon.

Voici l’ensemble des représentations des élèves dans ce padlet :

Padlet : Soleil et ombre (PDF de 4.2 Mo)

Padlet présentant les représentations des élèves de l’ombre du gnomon provoquée par les rayons du soleil.

Se confirme pour les élèves, le soleil se modélise principalement par un cercle plus petit que la Terre.
A la lecture du texte de Cléomède, l’objectif est qu’ils prennent conscience de la validité de leur modèle et principalement l’une des propositions admises par Ératosthène :
Troisièmement, que les rayons envoyés de différents endroits du soleil sur différents endroits de la Terre sont parallèles ; en effet, les géomètres supposent qu’il en est ainsi ;

Texte Cléomède Eratosthène (PDF de 9.6 Mo)

Extrait du texte original de Cléomède rapportant la découverte d’Eratosthène.

Les élèves ont vite accepté et compris la nécessité d’admettre cette représentation pour arriver à déterminer la circonférence de la Terre.
Une fois le modèle établi, les élèves, devant les notions mathématiques assez "simples", ont calculé la circonférence de la Terre.

Les élèves et la modélisation

Le début de l’activité les a largement "amusés". Ils ont trouvé impensable que certains pensent que la Terre est plate. Cependant, le fait que les élèves ont rencontré des difficultés à expliquer pourquoi la Terre n’est pas plate est questionnant. Elle renforce l’idée de mettre en avant les représentations des élèves du monde qui les entoure. Ces interrogations ont été source de motivation.

On retrouve ces problématiques dans la modélisation du Soleil perçue par de nombreux élèves comme plus petit que la Terre. Il paraît important de faire collaborer les élèves sur ce point afin de faire émerger les différents points de vue avant de donner la modélisation établie d’Ératosthène. Ce passage leur permet aussi de s’approprier la situation et de s’engager davantage plus marqué dans la tâche.

On pourra remarquer que l’analyse du texte se retrouve simplifié par la manière dont la situation est abordée dans les questions. Le problème d’unité (les stades) n’a pas été évoqué et n’a donc pas constitué une difficulté pour les élèves.

La collaboration entre élèves a permis de critiquer le sens des représentations. On distingue la différence entre croyances et sciences. Les élèves admettent ils que la Terre est ronde ou ont ils cherché à le vérifier ?

La démarche proposée dans cette tâche de modélisation illustre bien la démarche scientifique attendue dans les programmes :

Ce schéma propose la démarche scientifique intégrant pleinement la modélisation.

Prolongement et perspectives

A la suite de l’étude 1, j’ai proposé une synthèse qui a permis de mieux comprendre l’intérêt de s’interroger sur la forme de la Terre.

Synthèse La terre est ronde (PDF de 129.1 ko)

Synthèse présentant l’évolution des représentations de la Terre à travers l’histoire.

Cette synthèse permet aussi de comprendre les difficultés des élèves à s’approprier les modélisations devant le temps qu’il a fallu à accepter la rotondité de la Terre.

A la suite de ce parcours, j’ai poursuivi les échanges avec l’apport de la méthode de triangulation utilisée par Delambre et Méchain. J’ai aussi travaillé les automatismes avec des QCM sous forme de Google forms dont voici un exemple :

Questionnaire La Terre (PDF de 367.8 ko)

Questionnaire type QCM proposée aux élèves pour vérifier les acquis.

Documents de référence :

Document professeur.e Soleil-Terre (PDF de 284.6 ko)

Document professeur.e : comment peut-on se représenter la Terre ?

Document élève Soleil-Terre (PDF de 185.8 ko)

Document élève : comment peut-on se représenter la Terre ?

Retour au Sommaire des TraAms "modéliser"