Comment analyser les règles de construction en architecture ? publié le 14/06/2020 - mis à jour le 09/04/2021
Sommaire des TraAms "modéliser"
Description de la tâche de modélisation
Problématique
Pour pouvoir étudier un dispositif, une situation, il est souvent nécessaire à partir d’observations de construire une transcription "parfaite" de celle-ci. L’étude de cette façade doit permettre de dégager des propriétés mathématiques. Il s’agit, dans cette tâche, d’accompagner les élèves vers une relation pourtant déjà donnée.
Niveau concerné
Classe de Seconde
Modèle(s) mathématiques utilisé(s)
Configurations géométriques, équations
Autres compétences mathématiques mises en jeu
Chercher/Calculer/Raisonner
Compétences numériques
Création de contenu
Nombre d’heures envisagées
Une séance d’une heure.
Démarche de l’enseignant
L’étude de bâtiments en architecture aboutit souvent à l’utilisation de configurations mathématiques. Il est souvent difficile d’en trouver qui permettent une transcription proche des représentations des élèves. Les cathédrales et les églises se prêtent bien à ce type de situations recherchées.
Une fois le bâtiment choisi, il convient de réfléchir à la manière de le proposer aux élèves. Doit-on leurs faire trouver des relations ? Doit-on leurs donner la relation ? Sait-on comment l’architecte a procédé pour concevoir ces façades ?
Le programme de seconde intègre pour une grande partie la mise en place des fonctions comme modèle mathématique. La compréhension de la notion de fonction est à requestionner. En effet, au cycle 4, les programmes du bulletin officiel du 26 juillet 2018 invitent les élèves à comprendre et utiliser la notion de fonction. Or, les élèves rencontrent des difficultés principalement dans la compréhension du vocabulaire : variable, fonction, image, antécédent. C’est pourquoi, le fait de revenir sur "la mise en fonction de" sous de nombreuses formes permet aux élèves de s’approprier davantage cette notion.
Description du déroulement de la séance
Les élèves sont invités tout d’abord à comprendre que pour reproduire une figure, il est nécessaire de l’analyser afin notamment de pouvoir trouver des relations entre des quantités. Cette étape permet notamment de faciliter la construction d’œuvres d’art telles que la fresque de Raphaël (Voir article introduction des Traams).
Cette question est source de motivation pour les élèves. Le fait de comprendre que la géométrie peut permettre de construire des tableaux de la Renaissance contribue à "raccrocher" certains élèves peu intéressés par les questions de mathématiques. Ils comprennent le besoin d’une analyse plus fine devant l’écart entre leur figure et celle de l’artiste.
Voici la représentation d’un élève qui illustre les différences entre la représentation mathématique attendue et la sienne.
Production d’un élève modélisant la fresque "L’école d’Athènes" du peintre Raphaël.
Une fois ces échanges établis et un travail de longue haleine sur la nécessité de mettre "en fonction de", ils ont commencé la tâche de modélisation.
Je précise que pour cette étude, les élèves avaient bien intégré que la diagonale d'un carré de côté a est $a\sqrt{2}$.
Ma volonté était donc de les laisser seuls face à la modélisation nécessaire pour reproduire la figure :
Façade étudiée dans la tâche de modélisation.
Une fois les consignes données, ils se sont engagés dans la construction d’une représentation. Comme je l’avais imaginé les élèves ont rencontré des difficultés, j’ai dû rapidement intervenir en insistant sur le fait de dégager des configurations géométriques connues.
Voici la modélisation d’un élève :
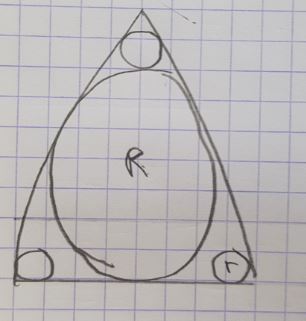
Production d’un élève modélisant la façade
J’ai alors ajouté un coup de pouce pour les aider : "il y a un rectangle à trouver".
Cela a permis d’orienter leurs démarches pour obtenir des modélisations plus proches de celle attendue.
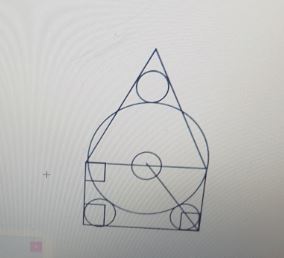
Production d’un élève modélisant la façade
J’ai alors proposé de mettre en relation les rayons des deux cercles. Ils ont constaté assez vite que ce type de figure n’est toujours pas exploitable. Nous sommes alors arrivés à la configuration attendue et nous avons pu réfléchir à l’organisation des étapes du raisonnement.
Voici le raisonnement rédigé par un élève :
Production dévoilant le raisonnement d’un élève autour de la modélisation retenue de la façade.
Nous avons réfléchi à la validité du modèle. En effet, pour aboutir à la relation attendue, il est nécessaire de construire un rectangle dont deux sommets sont aux extrémités inférieures des deux arcs de cercles. Ce qui ne semble pas être tout à fait vrai ici. Cela a permis aux élèves de critiquer le modèle et réfléchir à la démarche de l’architecte.
Les élèves et la modélisation
Tout d’abord, il convient d’insister sur le fait que les programmes en vigueur depuis 2018 constituent un frein dans la construction de la modélisation. En effet, la notion de tangente a disparu des programmes du cycle 4 et de seconde.
On peut s’interroger ici sur les modélisations des élèves souvent non exploitables et déconnectés des attendus en Mathématiques.
J’ai souhaité ici donner la relation et leur demander la modélisation adéquate. Cette approche se place dans la démarche scientifique où l’élève, par des observations, va s’approcher d’une modélisation pertinente. Nous avons pour habitude de demander la modélisation, voire, le plus souvent, de la donner puis guider les élèves vers une relation. Nous construisons donc des tâches très contextualisées dans un monde mathématique. Il convient donc de réfléchir à comment amener les élèves à construire un modèle à partir d’une analyse du réel.
On peut aussi se poser la question de l’intérêt de proposer ce genre d’exercice devant le nombre peu élevé d’élèves aboutissant à la modélisation attendue. Cependant, j’ai obtenu les effets suivants :
- Les élèves se sont tous engagés dans la tâche.
- Ils ont mesuré la complexité de modéliser une situation : elle doit permettre de dégager des propriétés.
- Ils ont compris les limites du modèle avec le problème de la "fin du rectangle".
- Une fois la modélisation établie, le nombre d’élèves ayant abouti à la relation a largement augmenté.
Cette démarche s’inscrit pleinement dans les recommandations du CNESCO (pdf de 1,2 Mo) en matière de différenciation :
- Garantir des objectifs ambitieux communs à tous.
- Prendre en compte la diversité des élèves dans les situations collectives.
Prolongement et perspectives
Il est possible une fois le raisonnement terminé de leur demander de reproduire la figure sur Geogebra. Ils seront d’ailleurs obligés de se servir de la relation pour la construire. L’outil "cercle centre-rayon" permet de réutiliser le rayon du grand cercle en utilisant son étiquette.
Voici le fichier obtenu :
Documents de référence
Document élève architecture et modélisation (PDF de 110.8 ko)
Document Élève : comment analyser les règles de construction en architecture ? - Académie de Poitiers.
Document professeur.e architecture et modélisation (PDF de 167.7 ko)
Document professeur.e : comment analyser les règles de construction en architecture ? - Académie de Poitiers.