Esprit critique et phénomènes aléatoires publié le 13/12/2023  - mis à jour le 17/05/2024

Fiche synoptique

Thématique

Phénomènes aléatoires : appréhender le hasard

Niveau concerné

Seconde

Problématique

Contenu

• statistiques, probabilités
• échantillonnage
• représentations graphiques : arbres, schémas
• algorithmique et programmation Python (fonctions, boucles, module random)

Nombre d’heures utilisées

• approche fréquentiste et obtention du jeu équitable : 4 heures
• simulations en salle informatique : 4 heures
• classe puzzle sur les raisonnements : 2 heures

Compétences du CRCN travaillées

• 1. Information et données :
  • 1.2 Gérer des données ;
  • 1.3 Traiter des données
• 3. Création de contenus :
  • 3.4 programmer ;
• 5. Environnement numérique :
  • 5.2 Évoluer dans un environnement numérique ;

Outils et ressources

• calculatrice
• tableur et fonctions ALEA.ENTRE.BORNES, NB.SI
• Plateforme Capytale pour la programmation Python
• brochure IREM n °61, pages 102 à 155
• Ensemble des documents utilisés pour la séquence :
  traam_esprit_critique_phenomenes_aleatoires_docs (Zip de 851.2 ko)

 Page suivante : "Narration de l’expérimentation (I) : la double approche des probabilités"

Narration de l’expérimentation, première partie : la double approche des probabilités

Le programme de mathématiques du cycle 4 précise les repères suivants en ce qui concerne les probabilités :

 
Les élèves ont travaillé sur les notions élémentaires de probabilité : expérience aléatoire, issue, événement, probabilité. Ils ont construit leur intuition sur des situations concrètes fondées sur l’équiprobabilité, puis en simulant la répétition d’épreuves identiques et indépendantes pour observer la stabilisation des fréquences. Ce travail est poursuivi en seconde en faisant appel à une version vulgarisée de la loi des grands nombres, qui permet de construire un modèle à partir de fréquences observées pour un phénomène réel.

Cette dernière approche des probabilités marque un changement significatif de perspective. La probabilité cesse d’être simplement une mesure théorique préalable au déroulement d’une expérience aléatoire pour devenir une estimation de la tendance caractérisant une expérience aléatoire, établie à partir de l’observation d’un grand nombre de réalisations de cette dernière. Cette dualité dans la conceptualisation de la probabilité découle des développements mathématiques survenus au cours des trois derniers siècles, en particulier du théorème fondamental de la Loi des Grands Nombres. Ce théorème, formulé initialement par Bernoulli dans Ars Conjectandi, contribue à concilier les deux approches. De plus, le Théorème Central Limite, découvert par Moivre et Laplace, affine cette connexion en précisant la convergence des fréquences observées vers la probabilité théorique.

En termes d’enjeux d’enseignement, il paraît donc essentiel pour la formation de l’esprit scientifique, de faire vivre ces deux approches antagonistes mais complémentaires dans nos classes :

• une approche "classique" ou "cardinaliste", fondée sur des considérations intuitives de symétrie ou de comparaison, dont les calculs de probabilités ne mobilisent que les propriétés physiques de l’objet probabilisé et s’effectuent a priori, donc indépendamment de l’expérience ;
• une approche "fréquentiste" ou "objectiviste", fondée sur l’expérimentation et les statistiques, dont les calculs de probabilités s’obtiennent a posteriori, comme limites des fréquences de réalisation de l’événement, quand le nombre d’épreuves tend vers l’infini.

Dans cette perspective, il fallait trouver une situation probabiliste pour laquelle les deux approches pouvaient être évoquées afin de montrer la non-contradiction de celles-ci et surtout leur complémentarité dans la construction d’un modèle représentant la situation.

Une situation déclenchante pour confronter les opinions

Le choix s’est arrêté sur la situation fournie par la projection de la planche suivante, extraite de la bande dessinée Astérix et le devin (Goscinny et Uderzo, 1972) :

Extrait de la bande dessinée "Asterix et le devin", Goscinny et Uderzo, 1972 (cliquer sur l’image pour l’agrandir)

Après un temps de réflexion, l’interrogation a porté sur le choix du "devin" :

• Avait-il intérêt à choisir le 7 s’il ne voulait pas passer pour un devin ?
• Y-a-t-il des sommes plus "probables" que d’autres ? Si oui, dans quelles proportions ?

Un certain nombre d’élèves a spontanément répondu qu’il n’y avait pas de meilleur choix parmi les sommes possibles et que les issues étaient équiprobables. Ces premières réponses illustrent un biais cognitif bien connu des psychologues : le biais d’équiprobabilité, engendré par une mauvaise application du principe d’équiprobabilité, et qui consiste à penser qu’en l’absence d’information, tous les cas ont la même probabilité de se produire et que « le hasard implique nécessairement l’uniformité ».
Ces premières affirmations ont vite été contredites par quelques élèves qui ont justifié leur intervention en considérant les décompositions possibles des différentes sommes : pour la somme 2, il n’y a qu’une seule possibilité (1+1) alors que pour la somme 7, il y a 3 décompositions (1+6, 2+5, 3+4)
Ces arguments ont permis de répondre rapidement à la première interrogation mais le questionnement s’est poursuivi sur le cas de sommes dont le nombre de décompositions semble identique (6 et 7 qui possèdent "a priori" 3 décompositions chacune).
Je leur alors demandé comment faire pour vérifier cette hypothèse et un élève a alors proposé de réaliser concrètement l’expérience aléatoire en faisant des séries de lancers de deux dés.

Expérimenter : l’épreuve du réel

Les élèves ont donc été invités à se regrouper en binômes puis à lancer 100 fois deux dés, à relever les sommes obtenues puis à calculer la fréquence d’apparition de chaque somme.

La réalisation des lancers n’a pas posé de problème mais, sans surprise, le dénombrement des issues a été plus fastidieux. Les élèves devaient ensuite écrire leurs fréquences au tableau :

Relevé des fréquences à l’issue de l’expérimentation réelle

Cette exposition au tableau des différents échantillons a permis de mettre en évidence la variabilité du hasard et la notion de fluctuation d’échantillonnage. Les différences de fréquences entre certaines issues (la somme 2 contre la somme 7) a été confirmée mais la proximité d’autres sommes (6 avec 7) n’a pas permis de conclure.
Les élèves devaient ensuite envoyer leur réponses via un formulaire en ligne qui permettait de constituer un échantillon plus grand, de taille 1300. La constitution d’un échantillon de taille plus grand, dont on calcule les fréquences par moyenne des fréquences des échantillons envoyés, permet d’obtenir des informations plus précises mais la variabilité des fréquences ne permet pas encore de conclure.

Il leur est alors demandé comment on pourrait obtenir un échantillon de plus grand taille sans trop d’efforts et la solution informatique est rapidement suggérée : calculatrice, tableur, programme.

Simuler pour décider

Après avoir défini la notion de simulation, les élèves ont été lancés sur la constitution d’un échantillon de taille 100 à la calculatrice. La simulation par les fonctions aléatoires de la calculatrice est un peu plus rapide mais le décompte des issues demeure pénible et entaché d’erreurs de comptage.

Le passage au tableur a été vécu comme un soulagement car la procédure est entièrement automatisée. Cette séance de manipulation a permis de remettre en place des savoir-faire de base (formule, duplication) et a été l’occasion d’aborder des commandes plus spécifiques à la simulation (ALEA.ENTRE.BORNES, NB.SI).

De même, la taille des échantillons de chaque groupe a pu être augmentée sans effort, jusqu’à 50 000 et l’envoi par formulaire des fréquences de chaque groupe a permis de constituer un échantillon de taille 1 000 000, pour lesquels les fréquences offraient une certaine stabilité.

Pour terminer le parcours sur la simulation, il leur a été proposé de réaliser des échantillons grâce à un programme rédigé en langage Python dans l’interface Capytale. Les élèves ne connaissant pas le langage, l’introduction a été très guidée et la complétion des codes a été pilotée par le professeur :

Fiche de cours sur les fonctions informatiques et la simulation (PDF de 136.7 ko)

Fiche de cours sur les fonctions informatiques et la simulation

Cette première approche leur a permis d’appréhender le concept de fonction informatique et son implémentation en langage Python (mots clés def, return). En outre, il leur a été possible de constituer un échantillon de taille 2 000 000 en appelant successivement la fonction avec différentes valeurs du paramètre issue : frequence_deux_des(2, 2_000_000), frequence_deux_des(3, 2_000_000), ....
Bien entendu, ces appels successifs construisent des échantillons différents et les fréquences obtenues ne sont pas celles d’un échantillon unique : pour rendre cela possible, il aurait fallu stocker les 11 compteurs de sommes dans une liste mais cette notion informatique n’est vue qu’en première. Cette petite entorse a été passée sous silence car la taille des échantillons rendait cette différence négligeable.

De nouveau, l’envoi des réponses a mené à la constitution d’un échantillon collectif de taille 44 millions pour lequel une précision de l’ordre du millième a pu être atteinte.

Tableur de collecte des échantillons (OpenDocument Spreadsheet de 37.2 ko)

Tableur de collecte des échantillons

Lors de la séance suivante, en classe entière, un bilan complet a été établi sur les deux séances informatiques précédentes et l’affichage des dernières fréquences obtenues sur le "gros" échantillon ont permis de mettre en évidence des symétries et des rapports de proportionnalité. Ces considérations ont mené à l’émergence de la loi de probabilité et notamment, le dénominateur 36 comme nombre total d’issues :

Bilan des simulations et obtention de la loi de probabilité (cliquer sur l’image pour l’agrandir)

Réinvestissement de l’approche fréquentiste : détermination d’un jeu équitable

Les différences de probabilités constatées lors de l’obtention de la loi ont mené au prolongement suivant :

Ce questionnement proposé en demi-classe a mené à des protocoles différents selon les groupes :

• premier groupe : chaque joueur lance un dé et si la somme est paire, c’est le joueur A qui gagne, sinon c’est le joueur B ;
• second groupe : chaque joueur lance un dé et si la somme est comprise entre 7 et 10, c’est le joueur A qui gagne, sinon c’est le joueur B

Afin de vérifier la validité de leur proposition, je leur ai demandé de vérifier leur choix par une simulation. Les élèves ont alors repris leur script précédent sur Capytale et, en s’inspirant des fonctions déjà construites, ils ont défini deux fonctions :

• une fonction de simulation de partie partie qui simule le lancer de deux dés et renvoie le nom du gagnant selon la condition choisie ;
• une fonction de réalisation d’un échantillon test_equite qui simule un nombre de parties entré en paramètre et renvoie les fréquences de victoires de chacun des joueurs.

En reproduisant avec un peu plus d’autonomie une situation analogue à la situation initiale, les élèves ont commencé à acquérir des repères en langage Python et ont identifié les éléments caractéristiques d’une simulation : fonction informatique qui simule l’expérience aléatoire, fonction de réalisation d’échantillon s’appuyant sur une boucle, avec un test et une variable "compteur" qui s’incrémente à chaque nouveau succès).

Conclusion

Ce parcours "initiatique" sur les probabilités a permis aux élèves de confronter leurs représentations initiales à la réalité de l’expérimentation, réelle ou simulée. Le biais de probabilité mis en exergue en début de parcours a illustré la notion de biais cognitif et les limites de la cognition, ce qui a mené à dégager des stratégies pour les dépasser : la simulation propose alors une démarche intellectuelle objectivée par le recours à la technologie et la stabilisation des fréquences observées est une preuve concrète qui a convaincu une majorité d’élèves.
Cette preuve par l’expérimentation a constitué un premier exemple de mise en œuvre de l’esprit critique face aux phénomènes aléatoires : notre intuition probabiliste peut nous tromper et il est indispensable d’apprendre à distinguer les interprétations validées par l’expérience, les hypothèses et les opinions liées à nos croyances.
Pour emporter la conviction des élèves et montrer la cohérence et la convergence des approches classique et fréquentiste, la représentation de l’expérience aléatoire sous la forme d’un arbre des possibles a permis de retrouver la loi de probabilité établie auparavant de manière empirique.

Arbre de possibilités représentant le lancer de deux dés (cliquer sur l’image pour l’agrandir)

Ainsi, la démarche didactique par la double approche a eu pour effet de donner davantage de crédit à la simulation comme moyen de produire des preuves de qualité et comme un outil fiable d’aide à la décision. L’expérimentation par la simulation sera de nouveau sollicitée dans la deuxième partie de la séquence.

 Page suivante : "Narration de l’expérimentation (II) : le problème des partis revisité"

Narration de l’expérimentation, deuxième partie : le problème des partis revisité

Présentation

Pour cette activité, je me suis inspiré d’un travail mené par l’IREM de Paris en 1986 (brochure IREM n °61, pages 102 à 155 et portant sur le problème des partis¹ dont voici une version (celle qui sera utilisée en classe) :

Ce problème possède une histoire car il fut l’objet de nombreuses propositions de solutions sans qu’aucune d’elles ne fasse véritablement consensus au sein de la communauté scientifique. Exposé pour la première fois par écrit en 1494 par Luca Pacioli, il sera étudié tour à tour par d’autres mathématiciens italiens : Jérôme Cardan en 1539, Niccolo Tartaglia en 1556 puis Lorenzo Forestani en 1603. En 1654, le problème sera proposé par Antoine Gombaud, chevalier de Méré, à Pascal qui entame alors une correspondance avec Pierre de Fermat au sujet de ce problème. Les calculs qu’ils développent peuvent être considérés comme les premiers calculs de probabilités même s’ils révèlent plus de ce qu’on appelle maintenant un calcul d’espérance mathématique.

En apportant une réponse définitive au problème des partis, cet échange épistolaire de l’été 1654 est passé à la postérité comme l’acte de naissance du calcul des probabilités. Toutefois, dans le contexte d’une expérimentation sur l’esprit critique, il m’a paru intéressant de revisiter les tentatives formulées au cours du 16^e siècle. En effet, cet ensemble de textes, lorsqu’on les rapproche, permettent à l’analyse de saisir toute une dynamique entre les solutions proposées et les critiques de certaines d’entre elles, tout un cheminement dans la compréhension du problème. Ce cheminement constitue un intérêt didactique qu’il m’a paru pertinent de soumettre à mes élèves pour solliciter leur esprit critique et les faire réfléchir sur la formation de leur jugement.

Une classe puzzle pour confronter et faire évoluer les représentations

Afin de favoriser les débats, les échanges d’opinions sur les solutions proposées par les différents auteurs, une organisation de type "classe puzzle" s’est imposée comme une modalité pertinente et motivante pour l’exercice de la pensée critique.
La classe puzzle est une technique d’enseignement inventée en 1971 par le psychologue Eliott Aronson. Elle permet un travail coopératif des élèves, où chacun acquiert des compétences d’expert, pour former les autres, et contribuer à la réalisation de la tache finale.
Je m’en suis inspiré pour établir l’organisation suivante prévue pour une séance d’1h30 :

• Temps 1 : présentation de l’activité et réflexion individuelle. Je présente la situation à la classe en plénière en insistant bien sur la problématique du jeu interrompu et la nécessité de réaliser un partage "juste" tenant compte du score au moment de l’arrêt du jeu. Je leur annonce ensuite le déroulement de la séance, en présentant le principe de la classe puzzle et les différents regroupements qui vont se succéder. Je lance l’activité en leur distribuant le document support ci-dessous. Pendant ce premier temps, ils disposent de 15 minutes de réflexion individuelle pour s’approprier la situation et proposer un partage de la mise.

Support de travail pour la classe puzzle (PDF de 62.5 ko)

Fiche de consigne pour la séance en classe puzzle sur le problème des partis (jeu interrompu)

Classe puzzle, temps 1 : réflexion individuelle

• Temps 2 : regroupement en groupes puzzle et confrontation des solutions individuelles
  Je les laisse ensuite se répartir librement en groupes de 4 ou 5 élèves (4 groupes de 5 et 2 groupes de 4). Pendant 15 minutes, sans intervention de ma part, ils confrontent alors leurs propositions au sein du groupe et si un élève est convaincu par l’argumentation d’un autre membre du groupe, il peut faire évoluer sa proposition initiale. Ils se répartissent ensuite les auteurs à étudier en groupes d’experts, selon le niveau de difficulté :
  • Solutions à une étoile : Luca (Pacioli) et Nicolas Tartaglia
  • Solutions à deux étoiles : Lorenzo Forestani et Jérôme Cardan
  • Solutions à trois étoiles : Pierre de Fermat et Blaise Pascal
    Solutions historiques à compléter en groupes d'experts (PDF de 87.5 ko)

    Solutions historiques à compléter en groupes d’experts

    Chaque groupe est tenu de traiter les deux solutions à une étoile, les deux solutions à deux étoiles et une des deux solutions à trois étoiles.

Classe puzzle, temps 2 : réflexion en groupes puzzle

• Temps 3 : regroupement en groupes d’experts et étude des solutions historiques
  Chaque groupe d’experts se voit attribuer une solution historique à compléter et dispose d’un tableau pour poser son raisonnement et écrire ses tentatives. Pendant cette phase de 20 minutes, je passe dans les groupes pour leur faire verbaliser leur compréhension du raisonnement proposé et je guide un peu les groupes bloqués.
  

  Classe puzzle, temps 3 : réflexion en groupes d’experts

• Temps 4 : retour en groupes puzzle et restitution des solutions étudiées
  Pendant cette phase de 20 minutes, chaque expert présente la solution qu’il a étudiée. Les autres élèves du groupe écoutent l’expert, prennent des notes, posent éventuellement des questions puis remplissent le cadre correspondant à l’auteur présenté. À la fin de ce temps d’échanges, tous les membres du groupe disposent de 5 solutions qu’ils peuvent désormais comparer.
  

  Classe puzzle, temps 4 : retour en groupes puzzle

• Temps 5 : réflexion individuelle et solution définitive
  Pour finir, les élèves disposent d’un quart d’heure de réflexion individuelle pour décider du partage qui leur semble le plus juste, après avoir évalué la qualité de chaque solution qui leur a été présentée. En fin de séance, ils envoient les versions successives de leurs solutions via un formulaire en ligne.
  

  Classe puzzle, temps 5 : conclusion individuelle et envoi des réponses

  Les réponses obtenues à ce sondage révèlent que :

• après la première phase de réflexion individuelle, la solution de Luca Pacioli, basée sur la proportionnalité des points acquis (7/12, 5/12), a été majoritairement donnée, dans 66 % des cas. Le reste des propositions relève soit de l’équiprobabilité (1/2, 1/2) soit de calculs incohérents pour un partage (somme des parts non égale à la mise totale). À noter qu’aucun élève ne propose la bonne solution (7/8, 1/8)
• à l’issue de la deuxième phase, 38% des élèves ont changé d’avis mais la solution majoritaire reste celle de Luca Pacioli, avec 88% des élèves qui la privilégient, cette solution perdant très peu d’adeptes de la première heure. Il est probable que les échanges entre pairs aient favorisé ce renforcement de la solution majoritaire par un biais comportemental bien connu : le biais de conformité, qui désigne notre tendance à agir et à nous aligner sur l’avis, pertinent ou pas, de la majorité, alors que l’on a initialement une idée différente.
• pour finir, après le regroupement entre experts, 46% des élèves ont modifié leur solution par rapport à l’étape précédente, mais, au final, la solution de Luca Pacioli reste majoritaire, avec 81% des réponses tandis que la "bonne solution" de Blaise Pascal ou Pierre de Fermat (7/8, 1/8) émerge timidement avec 8% de réponses.

 Page suivante : "Narration de l’expérimentation (III) : l’arbitrage par la simulation"

Narration de l’expérimentation, troisième partie : l’arbitrage par la simulation

À la fin de la séance en classe puzzle, j’ai volontairement omis de faire un temps de synthèse afin de laisser vivre les représentations de chacun et j’ai relancé le questionnement à la séance suivante et mis en doute la réponse majoritaire en faisant appel à l’argument de Nicolas Tartaglia pour critiquer la solution de Luca Pacioli :

Le doute s’est de nouveau installé chez mes élèves et j’ai pu mesurer le poids de la parole du professeur dans l’exercice de l’esprit critique des élèves : c’est le fameux biais d’autorité qui est la tendance à surévaluer la valeur de l’opinion d’une personne que l’on considère comme ayant une autorité sur un sujet donné. Au bout d’un certain temps de questions/réponses, les élèves ont finalement proposé de faire un programme sans vraiment savoir ce qu’ils allaient programmer mais ils avaient gardé en mémoire la première partie de l’étude dans laquelle la programmation/simulation avait permis d’accéder à la vérité.
Le raisonnement s’appuyant sur des répartitions proportionnelles aux parties déjà jouées ayant été mis en défaut, je leur propose un changement de paradigme en raisonnant sur ce qui aurait pu arriver si le jeu n’avait pas été interrompu et je leur demande d’imaginer les fins de jeux possibles à l’aide d’un arbre :

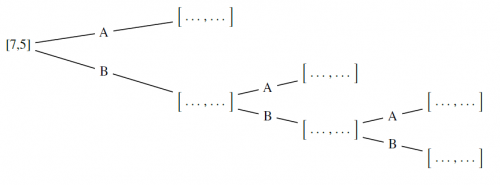
Arbre des fins de jeux possibles pour le problème du jeu interrompu (cliquer sur l’image pour l’agrandir)

Il reste ensuite à traduire ces éventualités en algorithme, avec une série de branchements conditionnels. Le passage de la structure en arbre à l’arborescence conditionnelle en langage Python a été guidée par un programme Python "à trous" enrichis de commentaires permettant aux élèves de compléter le programme avec une relative autonomie.

Fiche élève pour la simulation des fins de jeux (PDF de 101 ko)

Problème du jeu interrompu : fiche élève pour la simulation des fins de jeux.

Le jeu équitable (à partir du lancer de deux dés) ayant déjà été défini dans la première partie, la fonction deroule_jeu a ainsi pu être construite :

Fonction Python de simulation de fins de jeux (cliquer sur l’image pour l’agrandir)

Puis, avec l’expérience des autres simulations, la fonction de production d’échantillon simulation_jeux a été rapide à compléter :

Simulation des fins de jeux pour le problème du jeu interrompu

La simulation de plusieurs échantillons de grande taille (de l’ordre de 2 millions) a permis de faire apparaître la probabilité de victoire de chacun des joueurs (7/8, 1/8) :

Après simulation, le bilan en plénière a naturellement conduit à l’établissement de la solution mais certains élèves avaient encore des réticences face à cette valeur qui allait à l’encontre du raisonnement majoritaire. J’ai alors proposé de faire la démonstration de Pascal en faisant le fameux raisonnement "pas à pas" (récursivité), en réutilisant l’arbre des fins de jeux, mais en rajoutant les partages. Le principe de calcul consiste à commencer par la fin et remonter progressivement les calculs, en prenant comme gain de la partie en amont la moyenne des gains obtenus dans les deux issues possibles en aval :

Arbre des fins de jeux possibles avec partage de la mise (cliquer sur l’image pour l’agrandir)

Conclusion

L’enseignement des probabilités au lycée ne saurait faire abstraction des obstacles épistémologiques qui ont émaillé leur formalisation. Les erreurs historiques dans le problème des partis illustrent la difficulté de modéliser correctement une expérience aléatoire, même pour des mathématiciens reconnus à leur époque.
Selon les recherches récentes, cela semble tenir au fonctionnement de notre cerveau : celui-ci utilise des croyances (définies comme des estimations de probabilité) pour traiter les informations sensorielles et décider les actions à réaliser. Or celles-ci sont construites sur l’expérience personnelle et l’intuition qui en résulte est très souvent entachée de biais cognitifs (comme par exemple le biais d’équiprobabilité citée en début d’article) ou d’heuristiques de jugement (raccourcis cognitifs, généralement efficaces, qui visent à simplifier les opérations mentales).
Il n’est donc pas étonnant de retrouver des raisonnements probabilistes erronés chez des élèves de seconde dont l’appréhension rationnelle du hasard est encore en construction.
Afin d’acquérir des procédures robustes dans les démarches de résolution de problèmes probabilistes et par là même, développer son esprit critique face à des situations aléatoires, le choix s’est porté sur une activité collaborative favorisant les conflits socio-cognitifs (classe puzzle) afin de multiplier les confrontations de points de vue, qu’ils viennent des camarades ou des solutions historiques étudiées en groupe d’experts.
Ces regards croisés sur un même problème ont clairement généré des questionnements mais l’enquête qui a suivi a montré que les représentations initiales ont peu bougé malgré les doutes. Le recours à la simulation a eu davantage d’impact sur les opinions car il constitue une preuve plus tangible, produite par une expérimentation réalisée un grand nombre de fois : la répétition renforce la conviction. Cette approche expérimentale a convaincu les élèves sensibles au concret tandis que la démonstration finale par la méthode de Pascal a davantage séduit les élèves au fonctionnement plus rationnel. Il ressort donc de cette étude sur les probabilités que, pour faire bouger les représentations des élèves, il convient de favoriser la mise en débat et diversifier les approches.

Prolongement : programmation des probabilités théoriques

En fait, la démarche de Pascal dans la méthode "pas à pas" est algorithmique, et mène, si on la formalise de manière plus actuelle, à un algorithme récursif.
Il pourrait être intéressant, pour des élèves du cycle terminal, de le formaliser et de montrer que son implémentation dans un langage de programmation comme Python s’avère simple et élégante.

Partant d’un jeu équitable qui se gagne en $n$ parties, on considère deux entiers naturels $a$ et $b$ compris entre $0$ et $n$ (car il y aura au maximum $n$ parties) non tous deux égaux à $n$.
On note $p(a,b)$ la probabilité de victoire finale de A quand il a gagné $a$ parties et que B en a gagné $b$ : cette probabilité correspond alors à la fraction du pot qui reviendra à A en cas d’arrêt de la partie à l’état $[a,b]$. Pour retrouver la somme qui revient à $a$, il suffira alors de multiplier le montant du pot (deux fois la mise de chaque joueur) par $p(a,b)$.

Pour construire une fonction récursive, on étudie d’abord les cas de base :

• si $a=0$ et $b=n$, alors $p(a,b)=0$ ;
• si $a=n$ et $b=0$, alors $p(a,b)=1$

Ensuite on étudie la "remontée" de cas en considérant l’état de jeu en amont : on sait que $p(a,b)$ se calcule en faisant la moyenne des deux cas possibles :

• une victoire de plus pour A, de probabilité $p(a+1,b)$
• une victoire de plus pour B, de probabilité $p(a,b+1)$

On a donc la relation de récurrence : $p(a,b)=\dfrac{1}{2}p(a+1,b)+\dfrac{1}{2}p(a,b+1)$

et on obtient l’algorithme récursif suivant, implémenté en langage Python :

Pour une cible de 8 parties gagnantes, avec un état [7, 5], cela correspond à l’expérimentation en classe et on retrouve bien la probabilité de victoire pour A :

En revanche, dès que le nombre de parties à atteindre devient important, le nombre d’appels récursifs devient trop élevé et provoque une erreur de dépassement de capacité de récursions.
Par exemple, l’appel partis(100,3,4) ne répond pas.

Pour contourner cette limitation, il est possible de construire une version itérative du calcul en stockant les résultats intermédiaires dans un tableau dont le remplissage s’appuie sur la relation de récurrence :

Tableau de programmation des états du jeu (cliquer sur l’image pour l’agrandir)

Et on a de manière très rapide :

Pour les enseignants intéressés, une étude plus complète est proposée ci-dessous :

Problème des partis : étude globale (PDF de 204.8 ko)

Problème des partis : étude globale à destination des professeurs