TraAM 2017-18 : La boite de conserve publié le 24/05/2018 - mis à jour le 28/12/2019
Caractéristiques du scénario
Thématique
Construire la notion de fonction en programmation Python.
Niveau concerné
Classe de seconde. Même si l’on revient sur la dépendance d’une grandeur en fonction d’une autre, la notion de recherche du minimum ne permet pas la réalisation en fin de cycle 4. Il est cependant possible de le réaliser en première ou en terminale.
Compétences mobilisées
Modéliser (traduire en langage mathématique la situation de la boite de conserve), Calculer (appliquer des techniques et mettre en œuvre des algorithmes), Représenter (Choisir un cadre pour traiter un problème).
Problématique
Comment optimiser la surface de fer d’une boite de conserve ?
La volonté de cette activité est d’intégrer l’algorithmique et la programmation dans les contenus mathématiques proposés afin d’accompagner la modélisation.
L’objectif majeur est de montrer comment construire une fonction en programmation Python mais aussi comment l’exporter dans d’autres programmes. Ce travail s’inscrit donc pleinement dans l’objectif d’amener les élèves à la notion de “fonction” sous Python.
Nombre d’heures envisagées
Deux séances de deux heures espacées d’exercices techniques sur les fonctions en mathématiques.
Outils et ressources
Il semble préférable de travailler dans une salle informatique ou de mettre à disposition au minimum un poste pour 4 élèves.
Déroulement du scénario
L’idée est de proposer une approche algorithmique des fonctions. On peut tout à fait remplacer la question “mettre en fonction de” par “construire un programme qui calcule”. La démarche de l’élève sera finalement identique.
Autour de cette approche concrète (la boite de conserve "idéale") les élèves vont pouvoir manipuler des formules et la programmation Python afin de faire des interprétations hors mathématiques.
L’objectif principal reste de faire comprendre et d’utiliser la notion de fonction Python en mathématiques.
Mise en scène :
Les élèves font des recherches sur la construction et les normes des boîtes de conserve. Ils prennent conscience ici des enjeux économiques et structurels liés à la boite de conserve qu’ils ont tous manipulée. La mutualisation à l’aide du Padlet ( https://fr.padlet.com/ ) favorise le débat. Cela peut être gourmand en temps, il faut donc limiter ou lancer ce travail en fin de séance pour le finir pour la séance suivante.
Voici la production des élèves : https://padlet.com/chapellier/boiteconserve2017. On peut une fois de plus constater que ce travail collaboratif manque de diversité, les élèves ont du mal à apporter des éléments supplémentaires. Cependant, il permet à chacun de s’impliquer dans la situation proposée et de mettre en scène le sujet.

Bilan de la recherche d’un élève sur la fabrication des boîtes de conserves
La première étude :
L’utilisation du programme Scratch qui suit dans l’étude 1 s’explique assez rapidement et pousse les élèves à modéliser la situation. Les élèves ont compris la modélisation et l’univers Scratch les rassure. On peut d’ailleurs demander de la créer mais cela détourne de l’objectif de programmation en Python qui va suivre. Ce premier travail est favorisé par son aspect “débranché”.

Production élève suite à la modélisation de la boite de conserves
Ce travail m’a permis de revenir sur le vocabulaire des fonctions :

Bilan enseignant au tableau sur le vocabulaire des fonctions
Des questionnements sont apparus : comment est-il possible d’obtenir une surface plus petite pour un même volume ? Il faut alors convaincre...
L’idée de s’appuyer sur une animation Geogebra favorise la compréhension des élèves.
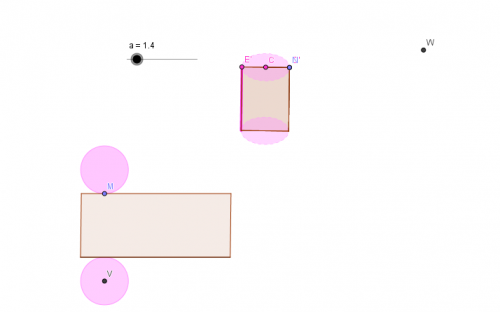
Production Geogebra facilitant la compréhension des élèves suite à la modélisation de la boite de conserves
Une fois le programme compris et la modélisation établie, ils ont effectué la comparaison entre Scratch et Python. Ce travail déjà réalisé dans les séances précédentes permet de rappeler l’intérêt de la programmation en Python. En effet, la notion de fonction Python évite la déclaration des variables et supprime les commandes "input" et "print" nécessaires à la programmation Scratch. Il faut néanmoins, inviter fortement les élèves à utiliser la console (le "shell") pour calculer les valeurs. Cette démarche n’est pas naturelle et les élèves sont tentés de faire demander au programme les variables. Lors de la recopie du programme, de nombreux élèves se trompent dans la syntaxe. Il m’a fallu pour certains programmes beaucoup de temps pour trouver l’erreur. L’aide de certains élèves maîtrisant le langage peut s’avérer précieuse.
On pourrait d’ailleurs proposer plus de programmes afin de tester si les élèves ont bien compris toute la syntaxe. Ici, la différence entre le périmètre et l’aire permet de vérifier la bonne compréhension de la programmation Python. La discussion sur la simplification de ce programme a suscité bien des discussions.
Les élèves ont alors calculé plusieurs valeurs et nous avons eu une première approche du minimum. C’est d’ailleurs le moment de confronter leurs valeurs avec celles obtenues avec un tableur :
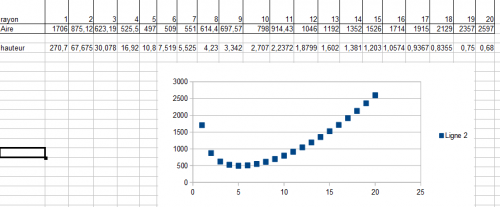
Document tableur présentant les résultats de la surface de fer pour les différents rayons choisis
Cette démarche ne les a d’ailleurs pas choqués, il a fallu que je leur demande comment l’on pourrait être plus précis.
La deuxième étude :
Après une nouvelle modélisation :
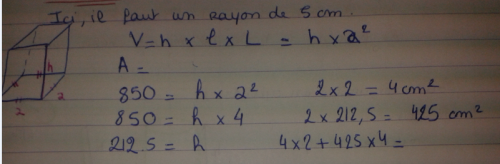
Production élève : Calcul de la hauteur de la boîte de conserves
Les élèves ont réalisé assez rapidement le programme sous Python. L’approche précédente a permis de les guider vers ce travail. Beaucoup ont d’ailleurs, comme expliqué précédemment, simplifié la fonction Python.

Production élève : fonction en langage Python qui calcule la surface de la boîte de conserves connaissant son rayon x.
Le fait de prendre une boite parallélépipédique permet de descendre le niveau de technicité mathématique et ainsi rendre plus accessible la programmation en Python.
L’explication du programme “minimum” a demandé en revanche un certain temps d’explication. Cela a d’abord commencé avec la nécessaire réflexion autour de l’ensemble de définition pour pouvoir donner les valeurs a et b à remplir dans cette fonction. Nous avons ensuite pris la fonction proposée en exemple pour déterminer son minimum et ainsi comprendre le programme avec un tableau de valeurs :

Document tableur présentant les valeurs qui permettent de comprendre le programme minimum en langage Python
Et, il a fallu que je m’appuie sur un tableau précisant les étapes de la boucle “while” et l’évolution de la variable a dans cette fonction. Je me suis d’ailleurs heurté à la traduction en anglais de while de certains élèves qui signifie : “tandis que”.
Il me parait encore aujourd’hui nécessaire de donner ce programme plutôt que de le faire construire car sa construction reste un attendu de terminale avec la méthode de balayage, néanmoins tout dépend du niveau de ses élèves en programmation. Le document d’accompagnement( http://revue.sesamath.net/IMG/pdf/170516-algorithmique-lycee.pdf ) propose d’ailleurs une autre version :

Fonction minimum en langage Python présentée dans le document d’accompagnement
L’utilisation du langage Python prend alors tout son sens, les élèves n’ont plu que par un simple copier-coller ré-utiliser la fonction minimum et l’insérer dans leur programme. Ils constatent alors la valeur minimale.
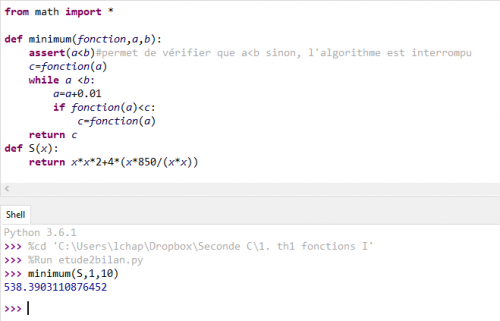
La valeur qui minimise la surface de fer obtenue avec l’algorithme en langage Python.
Cet algorithme est la composée des fonctions minimum et surface.
L’intérêt de cette démarche a montré aux élèves comment être plus précis et constitue un protocole réutilisable dans d’autres exercices.
Globalement, l’objectif a été atteint. Les élèves ont compris comment construire une fonction en programmation Python et son intérêt pour de futurs programmes. La technique de “mise en fonction de..” est travaillée sans cet éternel débat sur sa difficulté et les élèves n’ont pas fait les remarques habituelles sur l’arrivée du “x”. La structure d’une fonction en programmation Python leur permet de mieux comprendre les dépendances entre deux quantités.
D’autres approches sont possibles, on peut tout à fait laisser libre les élèves en donnant la problématique au départ. Cependant, l’objectif est multiple et en particulier de comprendre l’indépendance d’une fonction programmée en Python.
Les années précédentes, je demandais de le réaliser en programmation Algobox et cela ne permettait pas un travail de réinvestissement.
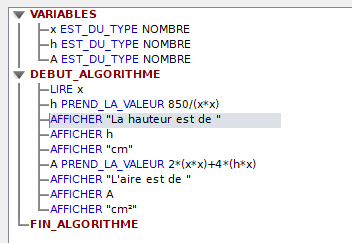
Programme en langage Algobox illustrant la plus-value du langage Python
Par ailleurs, les commandes AFFICHER et LIRE alourdissaient grandement le programme.
Enfin, la fonction minimum oblige les élèves à comprendre la notion d’ensemble définition.
Prolongements et évaluation :
Le premier prolongement possible est de demander aux élèves de modifier la fonction minimum pour qu’elle affiche aussi la valeur de x pour laquelle le minimum est atteint :
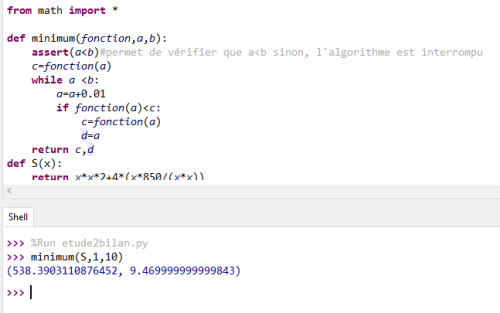
Prolongement de l’algorithme permettant de déterminer la valeur du rayon qui minimise la surface de fer. Il donne aussi la valeur du rayon
Voici un exemple de réutilisation de ce travail dans la suite de mon enseignement de ce travail avec l’exercice bien connu du “parallélogramme qui tourne” :
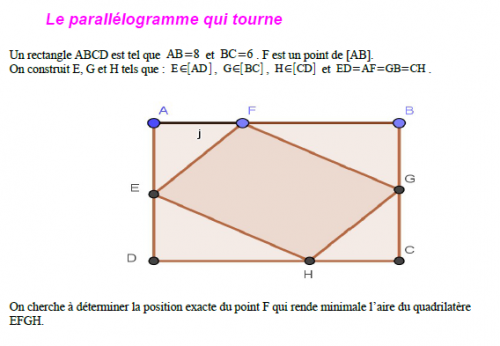
Exercice présentant le parallélogramme qui tourne
Voici ces vidéos qui présentent deux échanges que j’ai eu avec des élèves autour de cet exercice :
Ces vidéos d’accompagnement montrent les différents problèmes que l’on peut rencontrer lors d’une séance :
- La syntaxe du langage
- L’importance des décalages
- La nécessité de relancer le programme pour que la fonction soit connue
- L’utilisation du shell
- Comment gérer les messages d’erreur
Voici ce que j’ai donné en formative à la maison :

Devoir proposé aux élèves qui permet d’évaluer l’utilisation des fonctions en langage Python.
On peut remarquer ici que j’ai laissé l’élève choisir sa démarche. J’ai constaté malheureusement que peu d’élèves se sont tournés vers la programmation en Python. Je pense qu’il faut largement réinvestir et réutiliser cette fonctionnalité pour que cela devienne naturel pour les élèves.
Enfin, j’ai demandé de modifier cette fonction pour déterminer un maximum et je l’ai évalué.

L’algorithme qui détermine le maximum d’une fonction qu’il fallait compléter dans le devoir proposé aux élèves.
Voici quelques productions d’élèves :

Production réalisée par un élève dans le cadre de l’algorithme à compléter.

Production réalisée par un élève dans le cadre de l’algorithme à compléter.

Production réalisée par un élève dans le cadre de l’algorithme à compléter.
Documents de référence :
Document élève sur la notion de fonction en langage Python autour de la boîte de conserves.
Document professeur sur la notion de fonction en langage Python autour de la boîte de conserves.

