
Luxury at a small price - solution de l'énigme publié le 22/03/2013
Dans ce cryptarithme apparaissent dix lettres distinctes. On en déduit qu’il faut utiliser les 10 chiffres de 0 à 9.
L’égalité S + E = S entraîne que E = 0. On est finalement ramené au cryptarithme
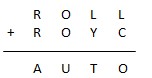
avec 8 chiffres et sans 0.
La recherche d’une solution où AUTO soit minimum impose de commencer par supposer R=1.
Etudions ensuite les valeurs possibles de O.
* O = 2 conduit à une impossibilité évidente, puisqu’on aurait aussi A=2
* O = 3
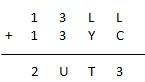
Dans ce cas, U vaut 6 ou 7. Les chiffres non utilisés sont 4,5,7 ou 6,8,9. Avec ces chiffres, il est donc impossible que L+Y n’entraîne pas de retenue. U vaut donc 7. En essayant de donner à L chacune des valeurs restantes : 4, 5, 6, 8, 9, on constate que l’on ne peut compléter l’addition jusqu’au bout.
* O = 4
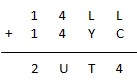
Dans ce cas, U vaut 8 ou 9. Les chiffres non utilisés sont 3, 5, 6, 7,9 ou 8. En essayant de donner à L chacune de ces valeurs, on constate que l’on ne peut compléter l’addition.
* O = 5 conduit à une impossibilité, car U ne pourrait prendre que les valeurs 0 ou 1 déjà utilisées.
* O = 6
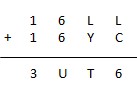
Dans ce cas, A vaut 3, et U vaut donc 2, ceci implique que L+Y se fasse sans retenue. Or les chiffres encore disponibles sont 4, 5, 7, 8 et 9, ce qui exclut une absence de retenue pour L+Y, compte tenu de la retenue du rand précédent.
* O=7
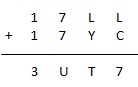
Dans ce cas, A vaut 3, et U vaut 4 ou 5. Essayons 4.
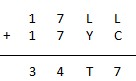
Les chiffres encore disponibles sont 2, 5, 6, 8 et 9. La seule façon d’obtenir 7 pour chiffre des unités de L + C est d’avoir L = 2 et C = 5, ou L = 5 et C = 2. Seule la première possibilité permet de compléter
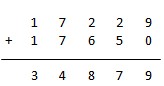
La plus petite valeur possible de AUTOS est donc 34879.

