Esprit critique et phénomènes aléatoires publié le 13/12/2023  - mis à jour le 04/05/2024

Narration de l’expérimentation, troisième partie : l’arbitrage par la simulation

À la fin de la séance en classe puzzle, j’ai volontairement omis de faire un temps de synthèse afin de laisser vivre les représentations de chacun et j’ai relancé le questionnement à la séance suivante et mis en doute la réponse majoritaire en faisant appel à l’argument de Nicolas Tartaglia pour critiquer la solution de Luca Pacioli :

Le doute s’est de nouveau installé chez mes élèves et j’ai pu mesurer le poids de la parole du professeur dans l’exercice de l’esprit critique des élèves : c’est le fameux biais d’autorité qui est la tendance à surévaluer la valeur de l’opinion d’une personne que l’on considère comme ayant une autorité sur un sujet donné. Au bout d’un certain temps de questions/réponses, les élèves ont finalement proposé de faire un programme sans vraiment savoir ce qu’ils allaient programmer mais ils avaient gardé en mémoire la première partie de l’étude dans laquelle la programmation/simulation avait permis d’accéder à la vérité.
Le raisonnement s’appuyant sur des répartitions proportionnelles aux parties déjà jouées ayant été mis en défaut, je leur propose un changement de paradigme en raisonnant sur ce qui aurait pu arriver si le jeu n’avait pas été interrompu et je leur demande d’imaginer les fins de jeux possibles à l’aide d’un arbre :

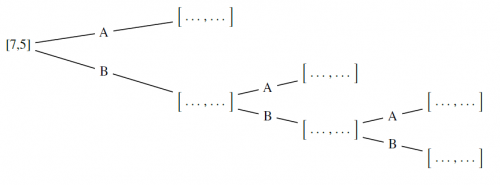
Arbre des fins de jeux possibles pour le problème du jeu interrompu (cliquer sur l’image pour l’agrandir)

Il reste ensuite à traduire ces éventualités en algorithme, avec une série de branchements conditionnels. Le passage de la structure en arbre à l’arborescence conditionnelle en langage Python a été guidée par un programme Python "à trous" enrichis de commentaires permettant aux élèves de compléter le programme avec une relative autonomie.

Fiche élève pour la simulation des fins de jeux (PDF de 101 ko)

Problème du jeu interrompu : fiche élève pour la simulation des fins de jeux.

Le jeu équitable (à partir du lancer de deux dés) ayant déjà été défini dans la première partie, la fonction deroule_jeu a ainsi pu être construite :

Fonction Python de simulation de fins de jeux (cliquer sur l’image pour l’agrandir)

Puis, avec l’expérience des autres simulations, la fonction de production d’échantillon simulation_jeux a été rapide à compléter :

Simulation des fins de jeux pour le problème du jeu interrompu

La simulation de plusieurs échantillons de grande taille (de l’ordre de 2 millions) a permis de faire apparaître la probabilité de victoire de chacun des joueurs (7/8, 1/8) :

Après simulation, le bilan en plénière a naturellement conduit à l’établissement de la solution mais certains élèves avaient encore des réticences face à cette valeur qui allait à l’encontre du raisonnement majoritaire. J’ai alors proposé de faire la démonstration de Pascal en faisant le fameux raisonnement "pas à pas" (récursivité), en réutilisant l’arbre des fins de jeux, mais en rajoutant les partages. Le principe de calcul consiste à commencer par la fin et remonter progressivement les calculs, en prenant comme gain de la partie en amont la moyenne des gains obtenus dans les deux issues possibles en aval :

Arbre des fins de jeux possibles avec partage de la mise (cliquer sur l’image pour l’agrandir)

Conclusion

L’enseignement des probabilités au lycée ne saurait faire abstraction des obstacles épistémologiques qui ont émaillé leur formalisation. Les erreurs historiques dans le problème des partis illustrent la difficulté de modéliser correctement une expérience aléatoire, même pour des mathématiciens reconnus à leur époque.
Selon les recherches récentes, cela semble tenir au fonctionnement de notre cerveau : celui-ci utilise des croyances (définies comme des estimations de probabilité) pour traiter les informations sensorielles et décider les actions à réaliser. Or celles-ci sont construites sur l’expérience personnelle et l’intuition qui en résulte est très souvent entachée de biais cognitifs (comme par exemple le biais d’équiprobabilité citée en début d’article) ou d’heuristiques de jugement (raccourcis cognitifs, généralement efficaces, qui visent à simplifier les opérations mentales).
Il n’est donc pas étonnant de retrouver des raisonnements probabilistes erronés chez des élèves de seconde dont l’appréhension rationnelle du hasard est encore en construction.
Afin d’acquérir des procédures robustes dans les démarches de résolution de problèmes probabilistes et par là même, développer son esprit critique face à des situations aléatoires, le choix s’est porté sur une activité collaborative favorisant les conflits socio-cognitifs (classe puzzle) afin de multiplier les confrontations de points de vue, qu’ils viennent des camarades ou des solutions historiques étudiées en groupe d’experts.
Ces regards croisés sur un même problème ont clairement généré des questionnements mais l’enquête qui a suivi a montré que les représentations initiales ont peu bougé malgré les doutes. Le recours à la simulation a eu davantage d’impact sur les opinions car il constitue une preuve plus tangible, produite par une expérimentation réalisée un grand nombre de fois : la répétition renforce la conviction. Cette approche expérimentale a convaincu les élèves sensibles au concret tandis que la démonstration finale par la méthode de Pascal a davantage séduit les élèves au fonctionnement plus rationnel. Il ressort donc de cette étude sur les probabilités que, pour faire bouger les représentations des élèves, il convient de favoriser la mise en débat et diversifier les approches.

Prolongement : programmation des probabilités théoriques

En fait, la démarche de Pascal dans la méthode "pas à pas" est algorithmique, et mène, si on la formalise de manière plus actuelle, à un algorithme récursif.
Il pourrait être intéressant, pour des élèves du cycle terminal, de le formaliser et de montrer que son implémentation dans un langage de programmation comme Python s’avère simple et élégante.

Partant d’un jeu équitable qui se gagne en $n$ parties, on considère deux entiers naturels $a$ et $b$ compris entre $0$ et $n$ (car il y aura au maximum $n$ parties) non tous deux égaux à $n$.
On note $p(a,b)$ la probabilité de victoire finale de A quand il a gagné $a$ parties et que B en a gagné $b$ : cette probabilité correspond alors à la fraction du pot qui reviendra à A en cas d’arrêt de la partie à l’état $[a,b]$. Pour retrouver la somme qui revient à $a$, il suffira alors de multiplier le montant du pot (deux fois la mise de chaque joueur) par $p(a,b)$.

Pour construire une fonction récursive, on étudie d’abord les cas de base :

• si $a=0$ et $b=n$, alors $p(a,b)=0$ ;
• si $a=n$ et $b=0$, alors $p(a,b)=1$

Ensuite on étudie la "remontée" de cas en considérant l’état de jeu en amont : on sait que $p(a,b)$ se calcule en faisant la moyenne des deux cas possibles :

• une victoire de plus pour A, de probabilité $p(a+1,b)$
• une victoire de plus pour B, de probabilité $p(a,b+1)$

On a donc la relation de récurrence : $p(a,b)=\dfrac{1}{2}p(a+1,b)+\dfrac{1}{2}p(a,b+1)$

et on obtient l’algorithme récursif suivant, implémenté en langage Python :

Pour une cible de 8 parties gagnantes, avec un état [7, 5], cela correspond à l’expérimentation en classe et on retrouve bien la probabilité de victoire pour A :

En revanche, dès que le nombre de parties à atteindre devient important, le nombre d’appels récursifs devient trop élevé et provoque une erreur de dépassement de capacité de récursions.
Par exemple, l’appel partis(100,3,4) ne répond pas.

Pour contourner cette limitation, il est possible de construire une version itérative du calcul en stockant les résultats intermédiaires dans un tableau dont le remplissage s’appuie sur la relation de récurrence :

Tableau de programmation des états du jeu (cliquer sur l’image pour l’agrandir)

Et on a de manière très rapide :

Pour les enseignants intéressés, une étude plus complète est proposée ci-dessous :

Problème des partis : étude globale (PDF de 204.8 ko)

Problème des partis : étude globale à destination des professeurs