Algorithmique et racine carrée en seconde publié le 03/03/2020  - mis à jour le 19/03/2020

Un parcours autour des algorithmes d’approximations de racines carrées

Motivations

En classe de seconde, le statut particulier de $\sqrt{2}$ a été évoqué au début de l’année au moment de l’étude des nombres réels et son caractère irrationnel avait été mis en avant à ce moment là.

Lors du chapitre sur les fonctions de référence, l’idée était de faire le lien entre $\sqrt{2}$ et la fonction carré, en présentant ce nombre comme la solution positive de l’équation $x^2=2$. Lors de l’étude des résolutions d’équations de la forme $x^2=a$, l’interrogation suivante fut proposée à la classe :

Ce questionnement était en lien avec le programme de mathématiques de seconde qui suggère l’étude de plusieurs algorithmes classiques proposant des approximations de nombres réels :

L’idée du parcours était donc de découvrir plusieurs méthodes d’approximations, s’appuyant sur les quatre opérations arithmétiques et sur les structures de bases de l’algorithmique.

Première approche avec GeoGebra et formalisation de l’algorithme de balayage

Après avoir brièvement présenté le fonctionnement d’une machine (ordinateur, calculatrice, ....) en mettant en avant les opérations logiques et arithmétiques qu’elle est capable d’exécuter et en insistant sur le fait que les calculs plus complexes reposent sur des séquences d’instructions organisées en programmes, la nécessité de traduire la recherche d’une racine carrée en algorithme a été posée.

Une première approche a été effectuée avec GeoGebra en s’appuyant sur la fonction carré. Dans cette activité, les élèves devaient :

• construire la courbe de la fonction $x\mapsto x^2$ ;
• créer un curseur $a$ débutant à 0, d’incrément initial 1 ;
• créer un affichage donnant la valeur de $a^2$ ;
• faire varier le curseur jusqu’à ce que le carré $a$ dépasse $2$, de sorte qu’un encadrement de $\sqrt{2}$ à l’unité soit obtenu ;
• affiner l’encadrement en réglant l’incrément du curseur à des valeurs de plus en plus petites

Un temps de synthèse a alors été proposé pour faire émerger la structure algorithmique sous-jacente : un balayage régulier de l’intervalle $[0\,;\,+\infty[$, d’un pas donné, qui se poursuit tant que le carré du curseur n’avait pas dépassé 2 : $x^2<2$.
La formalisation de ce mécanisme n’a pas été immédiate et la modélisation a bloqué sur deux points :

• formalisation d’une variable pas qui devait gérer le pas du balayage : les réglages successifs de l’incrément du curseur devait mener à l’émergence de cette variable mais tous les élèves ne l’ont pas perçu ;
• incrémentation de la variable pas : la traduction de l’action on passe à la valeur suivante n’a pas été simple à traduire et l’affectation x <- x + pas est loin d’être naturelle. L’idée d’"écraser" le contenu d’une variable par une expression qui contient elle-même ce contenu a posé problème.

En revanche, la structure du tant que est assez vite ressortie mais les élèves l’ayant dans un premier temps traduite par le Répéter jusqu'à ce que vu au collège avec Scratch, la différence sur la condition d’arrêt a été l’objet de discussions.

Une animation GeoGebra a ensuite été projetée au tableau afin de clarifier les propos et favoriser la représentation mentale de la situation. La visualisation de plusieurs simulations a permis de renforcer la perception de l’algorithme et les invariants du problème :

Algorithmes de balayage

Balayage à pas constant à partir de 0

La suite s’est déroulée sur machine, avec l’emploi du langage Python. L’algorithme ayant été défini auparavant, son implémentation n’a pas posé problème, mise à part la difficulté habituelle liée à la gestion de l’indentation (voir exécution en ligne) :

Le résultat renvoyé par la machine

a quelque peu dérouté les élèves et ce fut l’occasion de revenir une nouvelle fois sur la gestion des nombres (affichage, stockage en mémoire...) par une machine. Pour satisfaire l’attente des élèves, la fonction round, qui permet d’afficher un arrondi avec une certaine précision, a été introduite.

Généralisation et traduction par une fonction

Après avoir fait "jouer" les élèves avec le programme en leur demandant de modifier le pas, puis la valeur du nombre dont on veut la racine carrée, la manipulation s’est poursuivie par la recherche d’une fonction racine_balayage(nombre, nb_decimales) permettant de déterminer la racine carrée d’un nombre réel positif quelconque, à une précision choisie par l’utilisateur, ces deux éléments variables étant passés en paramètres de la fonction.

Le travail réalisé depuis plusieurs séances sur les fonctions a permis de construire rapidement l’enveloppe de la fonction :

• l’en-tête avec le mot-clé def : def racine_balayage(nombre, nb_decimales) ;
• l’instruction de renvoi du résultat avec le mot-clé return : return round(x-pas, nb_decimales), round (x, nb_decimales)

Entre ces deux lignes, on insère le bloc d’instructions venant du script précédent en l’adaptant à la généralité recherchée. Le code suivant a été obtenu par une majorité d’élèves de manière plus ou moins autonome (voir exécution en ligne) :

Appels de la fonction racine_balayage et limites

Les appels successifs de cette fonction pour divers nombres et diverses précisions a mis en évidence une lenteur de la réponse à partir d’une précision de 7 décimales. Le questionnement soumis aux élèves a fait émerger le problème dû au fait que l’algorithme repartait toujours de 0 donc balayait toujours l’intervalle $\left[0\,;\,\sqrt{\text{nombre}}\,\right]$, ce qui demandait un nombre de tours de boucle de plus en plus important quand la précision augmentait : pour un nombre donné, la distance à parcourir entre 0 et sa racine carrée reste la même mais comme le pas est plus petit, il y a plus de répétitions.

Afin de mettre en évidence ce phénomène, il leur a été proposé d’insérer un compteur dans la fonction racine_balayage : ce compteur, initialisé à 0, s’incrémente à chaque tour de boucle et compte ainsi le nombre de tours de boucle nécessaire pour obtenir l’encadrement souhaité (voir exécution en ligne) :

Les appels successifs avec la nouvelle fonction racine_balayage_bis mettent en évidence une propriété qui aurait pu être obtenue par un petit raisonnement : le nombre de tours nécessaire est de l’ordre de $\dfrac{\sqrt{\text{nombre}}}{10^{-\text{nb_decimales}}}$ et on dépasse le million de tours de boucle dès qu’on veut la racine carrée d’un nombre supérieur à 1 avec une précision de 6 décimales.

Amélioration de l’algorithme

Le défaut du départ à 0 ayant été mis en évidence, les élèves ont proposé spontanément d’utiliser une borne qui soit plus proche de la racine carrée cherchée.

En reprenant l’approche avec GeoGebra, la construction du nouvel algorithme, plus complexe, s’est faite de manière collégiale, avec le pilotage du professeur, et a abouti à la version usuelle de la méthode par balayage :

• mettre en place une deuxième structure répétitive : une boucle pour qui va exécuter l’algorithme précédent autant de fois que nb_decimales + 1 : 1 fois pour un encadrement à l’unité, deux fois pour un encadrement au dixième, 3 fois pour un encadrement au centième
• à chaque tour de boucle, déterminer l’encadrement par balayage en partant de la borne inférieure de l’encadrement obtenu au tour précédent.

Là encore, une animation GeoGebra semble avoir facilité la compréhension du problème :

Les élèves avaient alors à compléter un algorithme à trous traduisant la situation :

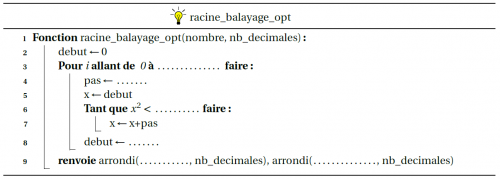
Cette image illustre l’algorithme à trous que les élèves devaient compléter afin de construire la nouvelle fonction de balayage.

L’encapsulation de la boucle tant que dans la boucle bornée pour a été bien comprise car elle validait la construction effectuée précédemment mais l’articulation entre la variable debut et la variable courante x, loin d’être évidente, a nécessité des explications supplémentaires.

La fonction racine_balayage_opt a été implémentée selon le script ci-dessous (voir exécution en ligne) :

Les difficultés d’implémentation se sont cristallisées sur la syntaxe et le fonctionnement de la fonction range : le dernier élément de la séquence fournie en paramètre ne fait jamais partie de la liste générée, ce qui oblige à rajouter un +1 pour avoir le nombre de répétitions souhaité.

Les appels comparés des deux fonctions de balayage ont rapidement mis en évidence (notamment grâce aux compteurs) l’amélioration du code, en terme de nombre de tours de boucle :

Conclusion

Cette séquence qui s’est déroulée sur 3 séances de TP hebdomadaires a permis d’aborder plusieurs aspects de l’activité algorithmique :

• résolution d’un problème par un algorithme, avec une modélisation s’appuyant sur la désignation de variables et la traduction d’une démarche par une structure algorithmique adaptée (boucle non bornée Tant que : notion de condition d’arrêt) ;
• encapsulation d’une structure algorithmique dans une fonction, avec identification des paramètres ;
• amélioration d’un code établi par la mise en place d’une deuxième structure répétitive (boucle bornée Pour : transition d’une étape à la suivante).

Ces éléments ont certes été travaillés avec un guidage serré du professeur mais les élèves ont bien perçu l’influence du code sur le nombre d’opérations effectuées pour résoudre un problème donné. Cette approche, très elliptique, de la notion de complexité algorithmique a été poursuivie lors d’activités complémentaires. (voir l’article En quête de racines, compléments).