Algorithmique et racine carrée en seconde publié le 03/03/2020  - mis à jour le 19/03/2020

Amélioration de l’algorithme

Le défaut du départ à 0 ayant été mis en évidence, les élèves ont proposé spontanément d’utiliser une borne qui soit plus proche de la racine carrée cherchée.

En reprenant l’approche avec GeoGebra, la construction du nouvel algorithme, plus complexe, s’est faite de manière collégiale, avec le pilotage du professeur, et a abouti à la version usuelle de la méthode par balayage :

• mettre en place une deuxième structure répétitive : une boucle pour qui va exécuter l’algorithme précédent autant de fois que nb_decimales + 1 : 1 fois pour un encadrement à l’unité, deux fois pour un encadrement au dixième, 3 fois pour un encadrement au centième
• à chaque tour de boucle, déterminer l’encadrement par balayage en partant de la borne inférieure de l’encadrement obtenu au tour précédent.

Là encore, une animation GeoGebra semble avoir facilité la compréhension du problème :

Les élèves avaient alors à compléter un algorithme à trous traduisant la situation :

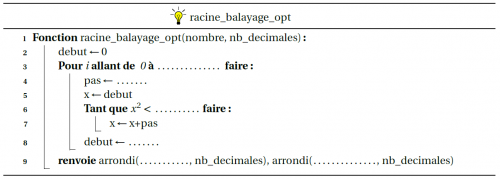
Cette image illustre l’algorithme à trous que les élèves devaient compléter afin de construire la nouvelle fonction de balayage.

L’encapsulation de la boucle tant que dans la boucle bornée pour a été bien comprise car elle validait la construction effectuée précédemment mais l’articulation entre la variable debut et la variable courante x, loin d’être évidente, a nécessité des explications supplémentaires.

La fonction racine_balayage_opt a été implémentée selon le script ci-dessous (voir exécution en ligne) :

Les difficultés d’implémentation se sont cristallisées sur la syntaxe et le fonctionnement de la fonction range : le dernier élément de la séquence fournie en paramètre ne fait jamais partie de la liste générée, ce qui oblige à rajouter un +1 pour avoir le nombre de répétitions souhaité.

Les appels comparés des deux fonctions de balayage ont rapidement mis en évidence (notamment grâce aux compteurs) l’amélioration du code, en terme de nombre de tours de boucle :

Conclusion

Cette séquence qui s’est déroulée sur 3 séances de TP hebdomadaires a permis d’aborder plusieurs aspects de l’activité algorithmique :

• résolution d’un problème par un algorithme, avec une modélisation s’appuyant sur la désignation de variables et la traduction d’une démarche par une structure algorithmique adaptée (boucle non bornée Tant que : notion de condition d’arrêt) ;
• encapsulation d’une structure algorithmique dans une fonction, avec identification des paramètres ;
• amélioration d’un code établi par la mise en place d’une deuxième structure répétitive (boucle bornée Pour : transition d’une étape à la suivante).

Ces éléments ont certes été travaillés avec un guidage serré du professeur mais les élèves ont bien perçu l’influence du code sur le nombre d’opérations effectuées pour résoudre un problème donné. Cette approche, très elliptique, de la notion de complexité algorithmique a été poursuivie lors d’activités complémentaires. (voir l’article En quête de racines, compléments).