Factorisations du niveau seconde ? publié le 12/07/2012
Intérêt du calcul formel.
But de ces exercices :
- Faire réfléchir les élèves sur les techniques de calculs à connaître pour résoudre une équation ou factoriser.
- Rendre naturel le recours à un logiciel de calcul formel lorsque les calculs sont trop compliqués ou hors programme.
- Savoir utiliser un logiciel de géométrie pour conjecturer des résultats.
Déroulement de la séance :
Ces quatre exercices sont proposés en module. Les élèves sont par groupe de deux ou trois et travaillent sur l’un des exercices imposés par l’enseignant. Une production écrite est rendue à la fin de la séance et un bilan est fait au cours suivant.
Consigne donnée :
« Faire l’exercice suivant en vous aidant si nécessaire de logiciels de mathématiques ou de la calculatrice pour répondre aux différentes questions. Des aides peuvent être demandées au professeur ».
Exercice n°1 : Hauteur d’une balle.
Enoncé :
Une balle est lancée. Au bout de x secondes, la hauteur atteinte par cette balle (en mètres) par rapport au sol est donnée par l’expression g(x) = -5x²+10x+15
1. A quels instants la balle est-elle à 15m ?
2. Quand la balle atteint-elle le sol (on suppose qu’elle ne rebondit pas) ?
3. A quels instants la balle est-elle à 18m ?
4. Quelle est la hauteur maximale atteinte cette balle ?
Travail des élèves :
- Pour la première question, les élèves répondent sans aide extérieure.
- Pour la seconde question, ils peuvent mettre le « 5 » en facteur : 5(-x²+2x+3)=0.
Discussion entre eux et avec l’enseignant pour repérer si oui on non, ils peuvent résoudre cette équation seuls.
Ils sont finalement obligés de faire appel à un logiciel de calcul formel : WxGéométrie (déjà utilisé en classe)
Deux possibilités :
Soit ils demandent directement la résolution de (-x²+2x+3)=0, soit ils demandent la factorisation de -5x²+10x+15.
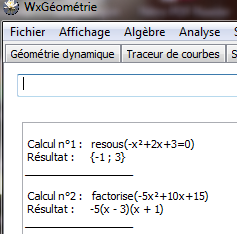
- Pour la troisième question, le même travail sera fait.
Il peut être demandé de vérifier la factorisation donnée par le logiciel pour travailler les développements avec des racines carrées
-5(x-1- ![]() (x-1+
(x-1+ ![]()
- Pour la dernière question, les élèves peuvent utiliser leur calculatrice pour obtenir un tableau de valeurs. Ils peuvent aussi utiliser WxGéométrie pour faire apparaître la courbe représentative de g. Pour se faire, il faut aller dans « traceur de courbes » puis régler la fenêtre en allant dans afficher puis « Réglage de la fenêtre ».Ils lisent graphiquement le maximum
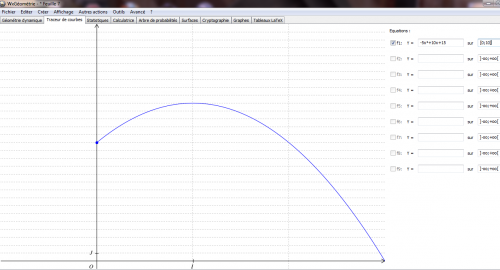
Constatant sur la courbe que 20 est le maximum de g, certains élèves travaillent sur le signe de "20 - g(x)", en tentant de factoriser cette expression sans l’aide du logiciel . D’autres choisissent de résoudre l’inéquation g(x)≤20. S’ils tapent "résous(-5x²10x+15<=20)", le logiciel WxGéometrie affiche ]-oo ;+oo[ (les élèves devront penser à réduire l’intervalle d’étude). Ils peuvent aussi taper " résous((-5x²10x+15<=20)et (x>=0))" , le logiciel WxGéometrie affiche alors [0 ;+oo[.
Page suivante : "Exercice n°2"

