La gravitation universelle : Lanceur de balle pour chien. publié le 30/12/2008

Pour une vitesse $v_0$ donnée, cette portée est maximale pour l’angle $\theta _{0m}$ suivant — là aussi passons sur le calcul :

La portée maximale est alors égale à :

Il apparaît donc que le paramètre $\frac{h}{h_0}$ régit la portée et que plus il est faible, plus on tend vers une portée maximale caractérisée par
_$\{ \theta _{0m}=\pi/4,L_{max}\hspace{0.1cm}=\hspace{0.1cm}{v_0}^2/g$ — celle calculée usuellement.
Pour le problème qui nous occupe, il est possible de lancer sans trop d’effort la balle à 10 m sans le lanceur. On peut alors en déduire que la vitesse de lancement est de l’ordre de 10 m.s^–1. Avec le lanceur, cette vitesse passe à quelque chose comme 20 m.s^–1 : la hauteur $h_0$ est donc de l’ordre de 20 m. Comme la balle est lancée d’une altitude d’environ 2,5 m, il s’ensuit que le rapport $\frac{h}{h_0}$ est de l’ordre de 0,125.

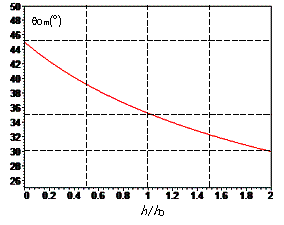
L’angle de lancement optimum est donc légèrement inférieur à 45° et la portée est alors d’un peu plus de 40 m, ce que l’observateur a pu vérifier sans trop se fatiguer.
En se fatigant un peu, il est possible d’augmenter notablement cette portée.
Remarque : bien sûr ces calculs ne tiennent pas compte de la traînée subie par la balle, cette traînée étant ici en première approche proportionnelle au carré de la vitesse.

Depuis le 20 mai 1990, le record du monde masculin de lancer du poids est détenu par l’américain Randy Barnes avec un jet de 23,12 m : on peut en conclure que le boulet a quitté sa main avec une vitesse d’environ 15 m.s^–1, son bras faisant vraisemblablement un angle d’environ 45° avec l’horizontale.