Modélisations de composants spécifiques de la chaîne d'information publié le 30/04/2020  - mis à jour le 17/11/2020

Les fonctions de la chaîne d’information, très souvent linéaires, peuvent être assimilées à de simples coefficients, ce qui, dans Sinusphy, est prévu par des composants génériques (ampli_kp, correcteur P, capteur...), mais il est avantageux d’avoir des modèles plus spécifiques qui font référence aux caractéristiques de la fonction. La prise en main par les élèves en est d’autant plus simple et devient une application du cours.

 Cet article va permettre de comprendre comment simuler, forcément en CAUSAL, des fonctions spécifiques comme des CAN -convertisseurs analogiques numériques- (ADC), des CNA -convertisseurs numériques analogiques- (DAC), des MLI -modulation de largeur d’impulsion- (PWM) et également un capteur de position (position sensor) connu sous le nom de potentiomètre de recopie (feedback potentiometer).

 Ces fonctions sont généralement décrites par leurs aspects techniques (quantum, résolution, format binaire, nombre de combinaison, codage, tension de référence...) mais plus rarement par leur fonction de transfert (coefficient directeur et décalage à l’origine). Le but est de réaliser des modèles qui déduisent l’équation reliant la sortie à l’entrée en fonction des valeurs des paramètres.

1- Création de 2 modèles paramétrables de CAN (ADC) :

 Sans parler de technologie, il existe 2 types de CAN :

• Les CAN unipolaires (intégrés dans les micro-contrôleurs) où la tension d’entrée ne varie qu’entre 0 V et une tension de référence (généralement la tension d’alimentation du micro-contrôleur : soit 5 V ou 3,3 V)
• Les CAN bipolaires (principalement utilisés dans le traitement de signal : acquisition du son, oscilloscopes numériques...) où le signal d’entrée est, par nature, centré autour de 0 V.

 Un CAN est principalement défini par le nombre de bits et la tension de référence (on néglige généralement le temps de conversion, forcément optimisé).

 Pour un CAN unipolaire, il est possible de déduire le nombre de combinaisons, le nombre maximum, le quantum (appelé aussi résolution) et le coefficient directeur de la fonction de transfert coef a = 1/quantum.

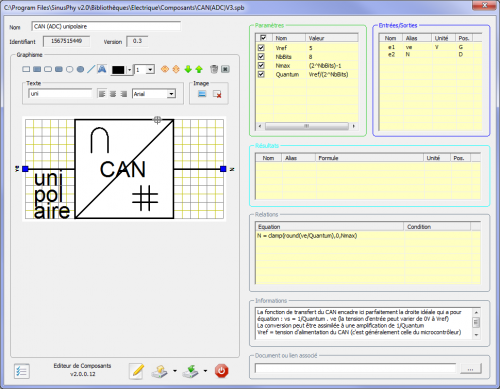
• Nmax = (2^NbBits)-1
• Quantum = Vref/(2^NbBits)
• N = clamp(round(ve/Quantum), 0, Nmax)
  La fonction round arrondit au nombre entier le plus proche, ce qui a pour effet d’obtenir une fonction de transfert idéale, c’est à dire entourant la droite de pente 1/quantum.
• La modélisation des composants de la chaîne d’information est principalement de type CAUSAL. Ceci est obtenu ici par l’utilisation de fonctions particulières (clamp, round) qui rendent l’équation parfaitement irréversible (une éventuelle modification de N ne pourra pas modifier la tension ve).

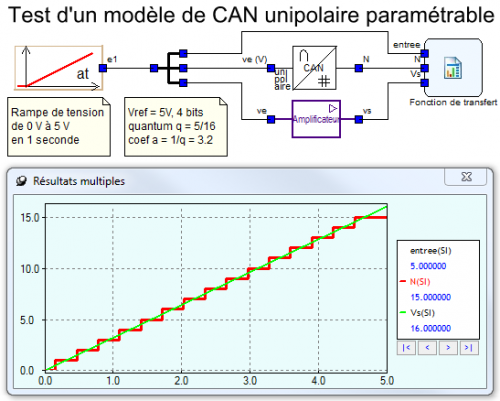
 Le schéma de test, ci-dessus, valide le calcul du quantum et du coefficient directeur (l’amplificateur témoin est paramétré avec coefficient directeur du CAN (coef a = 1/quantum)). Il montre ainsi que le CAN pourrait, en effet, être simplifié par un simple coefficient si le nombre de bits est suffisamment important (10 ou 12 bits en général) afin que la hauteur des "marches" soit de l’ordre du mV. Si les variations de l’entrée dépassent les limites, le modèle limitera N dans l’intervalle [0, Nmax].

 Dans sa version bipolaire, les équations sont légèrement différentes. Comme la valeur de N est signée, la moitié des combinaisons est positive ou nulle et l’autre moitié est strictement négative. Ici, le choix a été fait d’autoriser le signal d’entrée à varier, comme dans beaucoup de CAN bipolaires, de -Vref à +Vref, ce qui a pour effet de doubler le quantum (cela correspond à la solution classique qui consiste à transformer un CAN unipolaire en CAN bipolaire grâce à un montage à 2 résistances parfaitement identiques).

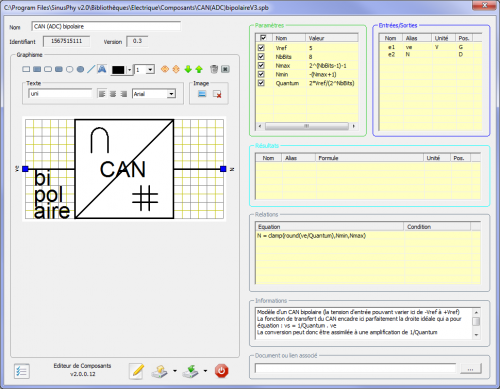
• Nmax = 2^(NbBits-1)-1
• Nmin = -(Nmax+1)
• Quantum = 2*Vref/(2^NbBits)
• N = clamp(round(ve/Quantum), Nmin, Nmax)
  La valeur du nombre entier N est limitée à l’intervalle [Nmin, Nmax].
  Exemple : Sur 10 bits, N restera compris entre -512 et +511 même si la tension d’entrée sort de l’intervalle [-Vref, +Vref]

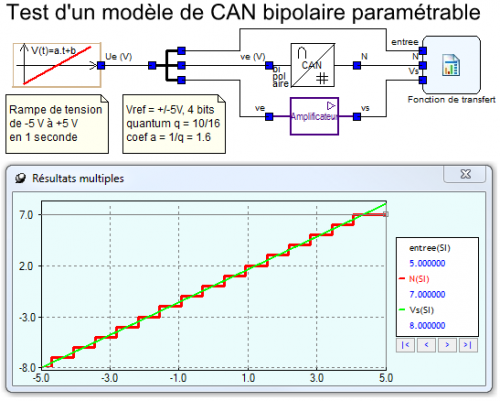
 Ici aussi, le schéma de test, avec son amplificateur témoin, permet de valider le calcul du quantum et du coefficient directeur.