L’année de lumière : Pythagore versus Thalès ou Eratosthène revisité. publié le 30/12/2008

Sur une plage, un homme dont les yeux sont à h=1,65 m du sol voit s’éloigner un voilier qui vient de quitter cette plage. Le voilier file vers le large à 5 nœuds de moyenne, soit 2,57 m.s^-1. Il met une demi-heure pour atteindre l’horizon.

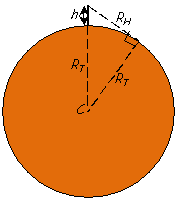
Cette observation permet d’obtenir une évaluation assez convenable du rayon terrestre. En effet, l’application du théorème de Pythagore à la figure ci-contre nous donne, désignant le rayon terrestre et celui de l’horizon vu par l’observateur :

Comme la hauteur h est naturellement très inférieure au rayon terrestre, on en conclut :

Soit avec les valeurs données :

Le même observateur se trouve en haut d’une falaise à L’Houmeau, près de La Rochelle : il observe les plages de la pointe d’Arcey en face de lui qui semblent être posées sur l’horizon.

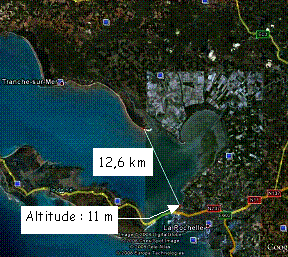
Document Google Earth

Le recours à Google Earth — ou à Géoportail du site de l’IGN — permet là encore d’en déduire le rayon terrestre. En effet, le point d’observation s’avère être à 11 m au dessus du niveau de la mer — les yeux de l’observateur en sont donc à 12,65 m — et la distance séparant l’observateur du point observé de 12,6 km.
Il s’ensuit, en utilisant la formule établie ci-dessus :

Bien sûr, il ne s’agit ici que d’une évaluation. Il faudrait en toute rigueur également tenir compte de la réfraction aérienne, si bien que les unités et les dizaines sont parfaitement superflues eu égard à l’incertitude des mesures. En effet, nous avons en prenant 1 cm d’incertitude sur h et 100 m sur  :

Rappelons qu’Eratosthène avait trouvé pour la circonférence terrestre quelque chose comme 39375 km — 250000 stades de 157,5 m — ce qui donne pour le rayon terrestre 6270 km.

L’incertitude relative de sa mesure est la somme de celle commise sur la mesure angulaire — on peut l’évaluer à 2 % — et de celle commise sur la mesure de la distance entre Sienne et Alexandrie — disons au mieux 1 %, voire plus.
En conséquence la méthode pythagoricienne n’a vraiment rien à envier à celle de Thalès. Notons pour finir que le rayon terrestre mesuré aujourd’hui varie entre 6378 km à l’équateur et 6357 km aux pôles, valeurs qui se trouvent dans l’intervalle de confiance des trois mesures précédentes — la première étant « limite » ce qui n’est pas pour surprendre, d’autant que, comme déjà dit, il n’a pas été tenu compte des effets de réfraction à l’horizon (mirage).