Échelle des longueurs : Comment mesurer la largeur du sillon d'un CD ou d'un DVD ? publié le 30/12/2008
Dans un CD (Compact Disc) ou un DVD (Digital Versatile Disc), l’information est stockée sur une piste d’alvéoles de de profondeur enroulée en spirale, la distance a entre deux alvéoles côte à côte étant de 1,6 µm pour le CD — parfois légèrement moins pour augmenter la capacité de stockage — et de 0,74 µm pour le DVD.

Lorsque la face d’un CD ou d’un DVD est présentée à la lumière blanche, la lumière réfléchie est irisée, donc décomposée. Le disque se comporte alors comme un réseau optique en réflexion. Si celui-ci est éclairé par un faisceau laser — monochromatique —, la lumière est alors réfléchie dans des directions bien déterminées.
Une partie de la lumière est réfléchie sur le faisceau incident si le disque est parfaitement perpendiculaire à ce dernier. On trouve aussi de la lumière réfléchie dans les deux directions θ±1 et éventuellement dans deux autres directions θ±2 plus écartées. La théorie des réseaux montre alors que — la longueur d’onde du laser étant désignée par λ et le pas du réseau par a :
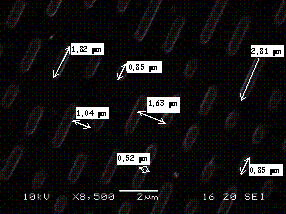
Vue d’un CD au microscope électronique - Document Wikipédia.
La mesure de ces angles par le biais de leur sinus permet ainsi d’atteindre la longueur a séparant deux alvéoles côte à côte — cf. figures :
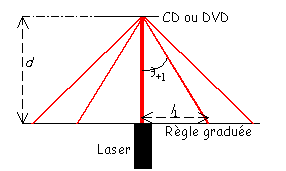
Mais à quoi sert de connaître le pas a d’un CD ? A déterminer sa capacité de stockage. Considérons par exemple un CD audio. Les alvéoles défilent à la vitesse constante de 1,22 m.s-1 sous la tête de lecture — vitesse standard imposée aux constructeurs de lecteurs CD —, ce qui implique une rotation du disque asservie à la position de ladite tête de lecture. Ainsi, le disque doit tourner plus vite quand elle est près du centre que lorsqu’elle est près de la périphérie — $\Omega = v/r \propto 1/r$.
La piste d’alvéoles étant comprise entre les rayons R1=2,25cm et R2=5,90cm et , le disque tourne à un peu plus de 500 tr.mn-1 quand la tête de lecture est près du centre et à environ 200 tr.mn-1 quand elle est à la périphérie. Calculons maintenant la longueur L de la piste d’alvéoles : la surface d’aire aL recouverte par cette piste spiralée correspond à l’aire comprise entre les rayons R1 et R2, d’où $aL=\pi (R^2_2-R^2_1)$.
La mesure optique nous donnant
$a\approx 1,6 \mu m$, il vient $L\approx 5840 m$ , soit près de 6 km !
La durée de musique enregistrable sur un tel disque est donc de $\Delta t \approx L/v= 5840/1,22 \approx80\hspace{0.2cm}minutes$ : un disque de concertos de Bach totalement gravé pris en exemple offre effectivement 79 minutes et 8 secondes d’écoute.
Et en termes d’octets, quelle capacité cela représente-t-il ? Les 1 du codage binaire correspondent au passage d’un creux d’alvéole à la surface du disque ou à celui de la surface au creux, les 0 étant traduits par un niveau constant. Or les plus petites alvéoles ont une longueur de l’ordre de 0,85 µm : c’est donc la « longueur » d’un 0 ou d’un 1. Ces 0 et ces 1 (bits) sont regroupés par groupe de 8 (octets, ou bytes en anglais), si bien que la « longueur » d’un octet est de $l_0\hspace{0.1cm}=\hspace{0.1cm}6,8\hspace{0.1cm}\mu m$.
Un disque CD-R 800MB peut ainsi stocker :
L’ordinateur indique effectivement une capacité de 856,775 mégaoctets : compte tenu des erreurs de mesure effectuées sur les longueurs, le résultat obtenu par le calcul est on ne peut mieux dans l’intervalle de confiance.
Si l’on désire enfin augmenter cette capacité, il faut diminuer le produit $l_{0}a$ : c’est ce qui permet de passer par exemple au DVD 4,7 GB ($4,7.10^9 bytes$). .
Pour en savoir plus, en n’oubliant pas de croiser les informations proposées sur Wikipédia, projet d’encyclopédie libre.

