Choisir un modèle de composant, le paramétrer, le valider et l'adapter aux besoins publié le 24/04/2020 - mis à jour le 17/11/2020
Partir d'un des composants les plus simples, un réducteur, pour comprendre les différentes démarches
Premier volet d’une série de 7 articles amenant à maîtriser la modélisation de composants de la chaîne d’énergie et de la chaîne d’information dans le but d’effectuer la simulation d’un asservissement numérique de position la plus précise possible afin que le comportement réel soit totalement prévisible.
Le choix d’un modèle de composant dans la bibliothèque et son paramétrage peuvent poser quelques problèmes aux élèves. L’enseignant peut donc être amené à adapter, dans le cadre d’une activité, un modèle pour simplifier son utilisation et son exploitation.
1- Position du problème
Le modèle du réducteur, objet de cette étude, existe en plusieurs versions :
Dans le dossier "Mécanique/Composants élémentaires" de la bibliothèque, il se trouve sous le nom de "réducteur élémentaire", le seul paramètre modifiable est le coefficient de réduction noté Kr.
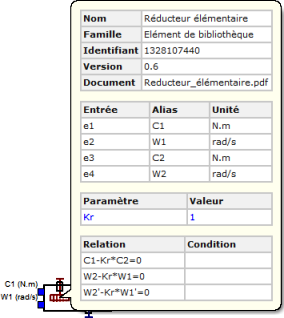
- Le composant est réversible,
- Il n’y a aucune perte, le rendement est de 100%,
- Le temps de réponse est nul, les modifications des grandeurs sont instantanées, ce qui peut poser des problèmes dans le choix du pas de calcul (le pas de calcul doit être suffisamment petit pour permettre de suivre les évolutions de toutes les grandeurs),
- Ce modèle simplifié n’est à utiliser qu’en phase de découverte, pour vérifier les relations fondamentales comme celles existant entre le couple de sortie et le couple d’entrée sur un composant idéal.
Dans le dossier "Mécanique/Composants complets", il se trouve sous le nom de "réducteur" et, comme on le voit, deux paramètres Jeq et mu sont ajoutés :
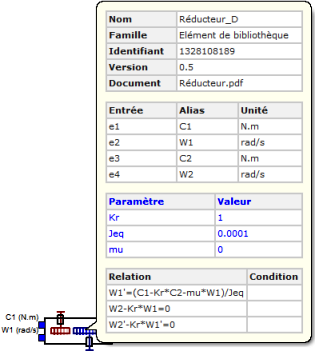
- Le composant est, bien sûr, réversible,
- Les pertes existent, sont réalistes et proportionnelles à la vitesse de rotation. Le paramètre mu, en N.m/rd/s, représente alors le coefficient de frottements visqueux (il est généralement noté f dans la littérature). Pour déduire mu, il faut estimer les pertes du réducteur réel. Pour cela, il faut partir de la connaissance du couple nominal en entrée C1nom (c’est généralement le couple nominal du moteur), de la vitesse nominale en entrée ω1nom (c’est généralement la vitesse nominale du moteur) et du rendement nominal du réducteur Rdnom estimé au point de fonctionnement [C1nom, ω1nom], en fonction de la technologie utilisée (le type d’engrenage, le nombre d’étages, la matière...).
- L’inertie Jeq, en kg.m², peut être calculée à partir des formes réelles des roues dentées et de la matière utilisée (ou plus simplement déduite de la maquette solidworks, à l’échelle, si la matière est renseignée) mais, comme sa valeur n’est pas critique, elle est souvent déduite d’un ordre de grandeur raisonnable pour la constante de temps τ(s) = Jeq/mu.
Méthode de détermination des paramètres mu et Jeq :
- Rendement nominal du réducteur Rdnom = 80% à ω1nom = 400 rd/s et pour C1nom = 0.1N.m
- mu = (1 - Rdnom) . C1nom / ω1nom = 50 . 10-6 Nm/rd/s
- Constante de temps réaliste : τ(s) = 20 ms
- Jeq = τ(s) . mu = 1 . 10-6 kg.m²

