Fonction dérivée et étude des variations d'une fonction (groupement A, B et C) publié le 21/10/2013
Pages : 12
Capacités
- Utiliser les formules et les règles de dérivation pour déterminer la dérivée d’une fonction.
- Étudier, sur un intervalle donné, les variations d’une fonction à partir du calcul et de l’étude du signe de sa dérivée. Dresser son tableau de variation.
- Déterminer un extremum d’une fonction sur un intervalle donné à partir de son sens de variation.
Connaissances
- Fonction dérivée d’une fonction dérivable sur un intervalle I.
- Fonctions dérivées des fonctions de référence
![]() , ( a et b réels),
, ( a et b réels), ![]() ,
, ![]() ,
, ![]() et
et ![]()
- Notation
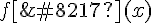 .
.
- Dérivée de
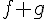 et
et 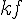 ,
, 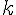 étant un réel non nul, à partir des fonctions
étant un réel non nul, à partir des fonctions 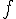 et
et 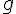 .
.

