Application des soldes publié le 15/09/2017 - mis à jour le 18/01/2019
Créer une application Android pour calculer des pourcentages
Présentation du projet
Objectifs
Faire créer aux élèves une application afin de lever le voile sur l’opacité du fonctionnement des objets numériques que les élèves manipulent au quotidien et accentuer leur compréhension du monde dans lequel ils vivent.
Mobiliser les connaissances sur les fonctions, la proportionnalité et la programmation pour réaliser des applications Android.
Niveau concerné
Fin de cycle 4.
Compétences mobilisées
| Mathématiques | Technologie |
|---|---|
| Chercher :
S’engager dans une démarche scientifique, observer, questionner, manipuler, expérimenter (sur une feuille de papier, avec des objets, à l’aide de logiciels), émettre des hypothèses, chercher des exemples ou des contre-exemples, simplifier ou particulariser une situation, émettre une conjecture. Tester, essayer plusieurs pistes de résolution. Décomposer un problème en sous-problèmes. |
Analyser le comportement attendu d’un système réel et décomposer le problème posé en sous-problèmes afin de structurer un programme de commande. (Concevoir, paramétrer, programmer des applications informatiques pour des appareils nomades.) |
| Modéliser :
Reconnaître des situations de proportionnalité et résoudre les problèmes correspondants. Traduire en langage mathématique une situation réelle (par exemple, à l’aide d’équations, de fonctions, de configurations géométriques, d’outils statistiques). |
Écrire un programme dans lequel des actions sont déclenchées par des événements extérieurs. |
| Représenter :
Choisir et mettre en relation des cadres (numérique, algébrique, géométrique) adaptés pour traiter un problème ou pour étudier un objet mathématique. |
Notions d’algorithme et de programme. Notion de variable informatique. |
| Raisonner :
Résoudre des problèmes impliquant des grandeurs variées (géométriques, physiques, économiques) : mobiliser les connaissances nécessaires, analyser et exploiter ses erreurs, mettre à l’essai plusieurs solutions. |
Déclenchement d’une action par un événement, séquences d’instructions, boucles, instructions conditionnelles. |
| Calculer :
Calculer en utilisant le langage algébrique (lettres, symboles, etc.). |
Problématique
Comment réaliser une application Android pour faire « Les soldes » ?
Comment trouver le prix d’un article soldé, quelque soit le prix et le pourcentage de solde ?
L’application Android finale (l’application « solde ») ici un exemple :
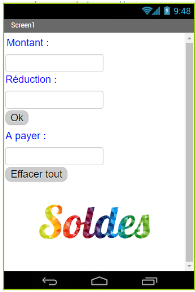
Déroulement de la séquence
Nombre d’heures envisagées par discipline
- une séance pour présenter le problème et préparer les calculs en mathématiques ;
- deux séances pour réaliser l’application (attention, si les élèves connaissent déjà AppInventor) ;
- sinon deux séances de plus pour une réaliser une autre application plus simple (la calculatrice).
Co-interventions envisagées (Discipline/Nombre d’heures) : Une heure pour expliquer le principe de l’EPI
La prise en main d’AppInventor par les élèves s’est déroulée en trois étapes :
- une première application du jeux des animaux ;
- création d’une calculatrice ;
- création de l’application sur les soldes.
Jeux des animaux
Afin de découvrir AppInventor, les élèves ont eu pour première mission de construire une application jouant des bruits d’animaux.
Exemple de ressources :
App Inventor ressource Numéro 6
Exemple de productions d’élèves :
Le jeu des animaux tuto AppInventor
Création d’une calculatrice
Afin de découvrir le fonctionnement des variables dans AppInventor, les élèves ont eu pour seconde mission de créer une calculatrice.
Voici un document complet présentant les modalités de création d’une calculatrice avec AppInventor par Claude Bodin :
Application pour les soldes
Pour finir, les élèves ont eu pour mission de réaliser une application facilitant la tenue d’un budget dans le cadre de soldes.
Exemples de productions d’élèves :
Application App Inventor pour calculer un pourcentage (pour les soldes)
Une application pour les soldes avec App Inventor
Prolongements éventuels (et/ou variantes)
Prendre en main AppInventor
Voici un article expliquant le fonctionnement d’AppInventor :
Créer des applications pour Android avec AppInventor
Piloter en bluetooth un robot Arduino
Dans le cadre d’un EPI avec la technologie, il est possible de piloter en bluetooth un robot. Voici un lien vers l’article correspondant :
Piloter un robot Arduino en bluetooth avec une application Android (AppInventor)

