Moyenne et médiane publié le 09/01/2016
Séquence à partir d'un extrait de journal télévisé
Préparation du terrain
Dans le chapitre sur les statistiques, nous avons revu les deux mesures de tendance que sont la moyenne et la médiane.
La moyenne est un paramètre connu depuis longtemps par les élèves mais ils ont souvent du mal à exprimer en quoi ce paramètre est représentatif d’une série statistique.
La médiane, abordée seulement en classe de troisième, est une notion récente dont le sens échappe encore à beaucoup d’élèves entrant en seconde. Outre les difficultés inhérentes à son calcul, la médiane leur apparaît souvent moins pertinente pour représenter une série.
L’idée de la séance était de leur montrer les différences entre ces deux nombres, notamment au niveau de la sensibilité aux valeurs extrêmes.
Diaporama de calcul mental
Pour préparer un peu le terrain, la séance débute sur un diaporama de calcul mental (voir document joint), dont le but est de réactiver les notions abordées lors des cours précédents et pour le professeur, d’en vérifier leur bonne assimilation.
Après une correction rapide et un sondage à main levée pour mesurer la réussite de chacun, je leur fais remarquer la proximité de la moyenne et de la médiane dans la série du diaporama.
Correction d’un exercice
Ensuite, la séance se poursuit avec la correction d’un exercice qui était à préparer à la maison (voir document joint). L’application ChingView permet dans cette situation de prendre un cahier d’élève en photo avec un smartphone puis d’envoyer cette photo vers le video-projecteur via un ordinateur. La correction s’appuie sur le travail de l’élève et permet de revenir sur la technique de détermination de la médiane d’une série discrète selon les cas pair et impair. Là encore, la proximité entre moyenne et médiane est encore mise en exergue.
Travail d’un élève :
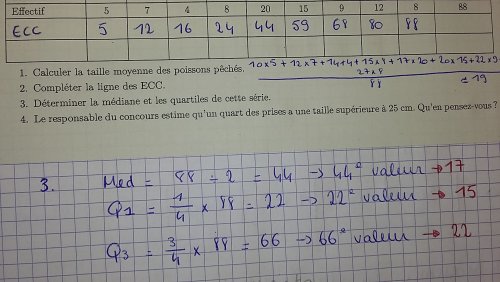
Visionnage de la video et travail
Ayant insisté sur ce voisinage moyenne/médiane, je leur propose alors de visionner un extrait de journal télévisé (JT de BFMTV du 31/03/13) ayant pour sujet le salaire des Français en 2011. Je leur demande de noter toutes les informations chiffrées contenues dans ce document de 40 s.
Après un premier visionnage, beaucoup d’élèves me demandent de repasser la video car ils n’ont pas eu le temps de tout noter. Il faudra en tout 3 passages pour qu’ils aient pu noter la majorité des données diffusées dans ce reportage.
C’est l’occasion de leur faire remarquer la grande quantité d’informations que peut contenir un reportage censé s’adresser au français moyen devant sa télévision.
Après avoir trié les informations, nous ne gardons que celles relatives à la moyenne et la médiane. L’écart significatif entre ces deux paramètres (2130 euros pour la moyenne contre 1712 euros pour la médiane) peut poser question, surtout après le travail préparatoire effectué. Certains élèves ont déjà une explication à fournir et évoquent le fait que la moyenne tient compte de tous les salaires, notamment les gros salaires qui tireraient la moyenne vers le haut.
Pour mettre en évidence cette sensibilité de la moyenne aux valeurs de la série, je leur propose de compléter des séries de salaires simples dont on imposait le minimum, le maximum et la médiane (en m’appuyant sur les valeurs du reportage) :
| 1100 | .......... | .......... | 1700 | .......... | .......... | 3400 |
|---|
| 1100 | .......... | .......... | 1700 | .......... | .......... | 3400 |
|---|
Les élèves ont mis un peu de temps avant de produire des séries satisfaisant les conditions. Ils sont d’abord partis un peu au hasard et ne tombaient jamais sur la moyenne demandée. En passant dans les rangs, je leur ai rappelé qu’une moyenne fixée avec 7 salaires imposait une valeur pour la somme des salaires. Finalement, un bon nombre d’élèves est parvenu à construire des séries répondant aux conditions. Ils ont vu sur ces deux exemples la nécessité de rapprocher leurs valeurs du salaire maximal pour espérer un salaire moyen élevé et inversement.
J’ai proposé un prolongement pour les élèves les plus rapides :
| 1100 | .......... | .......... | 1700 | .......... | .......... | 3400 |
|---|
| 1100 | .......... | .......... | 1700 | .......... | .......... | 3400 |
|---|
Après correction, on conclut que les séries proposées avaient toutes la même médiane mais que leur moyenne pouvait fortement osciller (entre 1685 euros et 2342 euros). La médiane est donc un paramètre "robuste" vis-à-vis des valeurs d’une série statistique alors que la moyenne est "sensible" aux valeurs de cette série, notamment les valeurs extrêmes.
Un prolongement possible aurait été de reprendre une des séries construites et de modifier le salaire maximal en le remplaçant par un très gros salaire. On aurait pu se rendre compte dans ce cas de la perte de représentativité de la moyenne.
Moyenne et médiane - Séquence à partir d’un extrait de journal télévisé.
Moyenne et médiane - Séquence à partir d’un extrait de journal télévisé.