
L'hôtel sangaku - Solution de l'énigme publié le 21/03/2015
Solution de l'énigme du jeudi 19 mars 2015 pour les élèves de troisième et de seconde
Voir l’énoncé de l’énigme
Solution
Considérons le point F tel que EDAF soit un parallélogramme.
EDAF est un parallélogramme qui a deux côtés consécutifs égaux (AD = DE = 5 cm), donc c’est un losange de côté 5 cm.
Les droites (AD) et (EF) sont parallèles et les droites (AD) et (BC) sont parallèles, donc (EF) et BC) sont parallèles.
AD = EF et AD = BC, donc EF = BC.
Le quadrilatère BCEF a donc deux côtés opposés parallèles et de même longueur, donc c’est un parallélogramme.
De plus, il a deux côtés consécutifs égaux (BC = CE = 5 cm), donc c’est un losange.
Il résulte donc que FE = FA = FB = 5cm.
Le centre du cercle est donc le point F et son rayon mesure 5 cm.
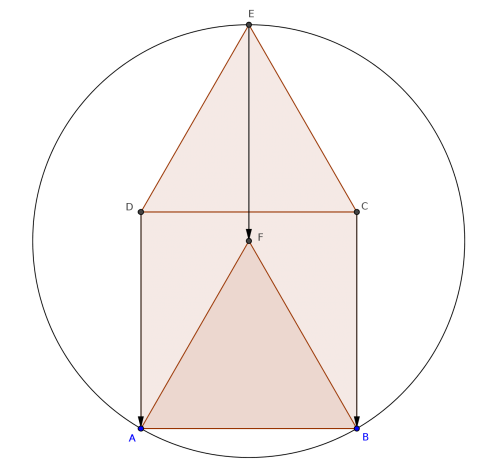
Figure pour résoudre l’énigme concernant l’hôtel Sangaku.

