Factorisations du niveau seconde ? publié le 12/07/2012

Exercice n°4 : Sapin de Noël.

Enoncé :

Pour réaliser des sapins en papier de base et de hauteur 8 cm pour décorer une table, on découpe un triangle isocèle de façon à ce que la surface restante représente 80% du triangle de départ.
 

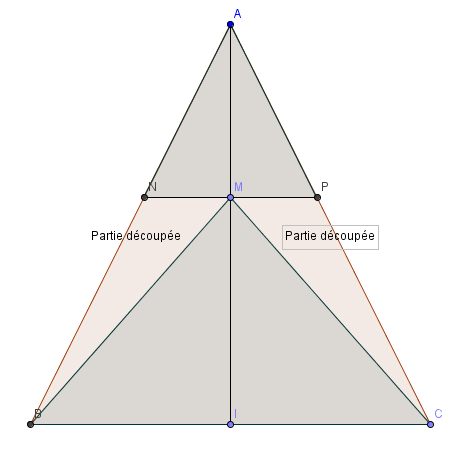
ABC est un triangle isocèle en A, I est le milieu de [BC]. M est un point de [AI].
La parallèle à [BC] passant par M coupe [AB] en N et [AC] en P.
 

Déterminer la position de M de façon que la somme des aires des triangles ANP et MBC soit égale à 80% de l’aire du triangle ABC.

Travail des élèves :

La figure à réaliser avec GéoGébra a posé quelques problèmes ainsi que le choix de l’inconnue. De plus, la configuration de Thalès n’a été repérée qu’avec l’aide de l’enseignant.
Pour répondre au problème posé, le logiciel WxGeométrie permet d’obtenir les valeurs exactes des solutions de l’équation x²-8x+12.8 = 0 à condition de l’écrire sans nombre décimal : x² - 8x + .
 

Le logiciel GéoGébra ne permet d’obtenir que des valeurs approchées de ces solutions. Et il est préférable d’utiliser la commande "racine". La figure obtenue avec ce logiciel conduit pour des raisons esthétiques, à ne retenir qu’une seule solution 4-, soit environ 2.21.

Bilan de l’activité :

Cette activité a permis aux élèves :

• d’apprendre à repérer les formes que l’on peut factoriser en seconde ( liées à une identité remarquable et/ou trouver un facteur commun). Par la suite, ils abordent mieux les factorisations ou les équations à résoudre.
   
• de progresser dans l’utilisation des deux logiciels GéoGébra et WxGéométrie, et savoir passer de l’un à l’autre suivant le problème posé.
   

Enoncés élèves (PDF de 137 ko)