Un exemple d'œuvre travaillée en classe de mathématiques publié le 16/03/2012  - mis à jour le 21/06/2017

Une histoire de formats

D’abord $\sqrt{2}$

Le chapitre sur les racines carrées a mis l’accent sur l’existence de nombres un peu particuliers, les nombres irrationnels. Après une approche historique du nombre $\sqrt{2}$, obtenu comme la longueur de la diagonale d’un carré de côté 1 unité, nous avons démontré en classe que ce nombre n’était pas décimal puis qu’il n’était pas non plus rationnel.
Nous avons ensuite poursuivi l’étude de ce fascinant nombre $\sqrt{2}$ en nous intéressant aux formats de rectangles. Nous nous sommes appuyés sur les formats de papier : A4, A3,... Nous passons du format A3 au format A4, en pliant des feuilles A3 en deux, puis du format A4 au format A5 en pliant également en deux une feuille A4.
L’exigence du format normalisé A est que les feuilles successives gardent le même "aspect", ce qui se traduit mathématiquement par la conservation du rapport $\frac{\mbox{longueur}}{\mbox{largeur}}$. Sous ces conditions, en partant d’une feuille $A_{n}$ de format $L\times \ell$, que nous plions en deux, la nouvelle feuille est au format $\ell\times \frac{L}{2}$ :

La conservation du rapport mène alors à l’équation :

$$\frac{L}{\ell}=\frac{\ell}{\frac{L}{2}}$$

soit :

$$\left(\frac{L}{\ell}\right)^2=2$$

Le nombre $\sqrt{2}$ apparaît alors comme la seule réponse de proportion conservant le format par pliage en deux.

Puis le nombre d’or $\Phi=\frac{1+\sqrt{5}}{2}$

On étudie ensuite un autre exemple de format de rectangle :
le rectangle d’or dont les proportions vérifient la définition suivante :
Un rectangle d’or est un rectangle dont les dimensions $L\times\ell$ sont telles que si on lui retire le carré formé sur sa largeur, le rectangle restant de dimensions $\ell\times(L-\ell)$ a le même rapport que le rectangle de départ.

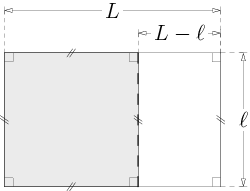
La conservation du rapport se traduit cette fois-ci par l’équation :

$$\frac{L}{\ell}=\frac{\ell}{L-\ell}$$

et qui donne l’équation du second degré :

$$\left(\frac{L}{\ell}\right)^2-\frac{L}{\ell}-1=0$$

Le nombre $\Phi=\frac{1+\sqrt{5}}{2}$, unique solution positive de cette équation est défini comme le nombre d’or.

 

---

Le nombre d’or en peinture

Après avoir demandé aux élèves de faire des recherches personnelles sur le nombre d’or, nous organisons une synthèse des domaines où intervient ce nombre et nous leur proposons de travailler sur un exemple contemporain : Le sacrement de la dernière Cène de Salvador Dali, réalisé en 1955.

Activité papier, crayon, calculatrice

La fiche jointe ci-dessous est distribuée et les élèves y répondent par équipe de deux. Cette activité fut l’occasion de retravailler plusieurs notions :

• prise de mesures et précision ;
• valeurs approchées et chiffres significatifs ;
• propriétés du rectangle et du carré ;
• tracés avec outils de géométrie, précision ;
• polygones réguliers : cas du pentagone.

Une heure entière y a été consacrée suivie d’une synthèse en plénière, avec le vidéoprojecteur et GeoGebra.

• fiche élève pour l'activité papier, crayon, calculatrice (PDF de 2.1 Mo)

  Ce document contient les consignes à suivre pour découvrir les caractéristiques mathématiques du tableau de Dali, avec les outils classiques de géométrie et la calculatrice.

  Activité sur poste informatique avec GeoGebra

  Faute de temps, cette activité n’a pu être réalisée. Le principe était de suivre les mêmes consignes mais sur le logiciel Geogebra, afin de comparer les deux approches. Par ailleurs, les élèves pouvaient ainsi se construire un fichier de présentation pour leur oral d’histoire des arts en utilisant la fonction navigation dans les étapes de construction de GeoGebra.

• fiche de consignes pour l'activité GeoGebra (PDF de 105.9 ko)

  Ce document contient les consignes à suivre sur GeoGebra pour découvrir les caractéristiques mathématiques du tableau de Dali.

• fichier GeoGebra pour les élèves (Fichier GeoGebra de 62.4 ko)

  Ce fichier GeoGebra est le support de départ sur lequel les élèves vont effectuer des calculs et des tracés pour découvrir les caractéristiques mathématiques du tableau de Dali.

• fichier Geogebra de synthèse (Fichier GeoGebra de 60.9 ko)

  Ce fichier contient le travail théoriquement fait par les élèves à l’issue de l’activité GeoGebra. Il pourra servir de support de présentation pour l’oral d’histoire des arts.