Un problème d'optimisation publié le 24/02/2011 - mis à jour le 30/08/2011
Appréhender la notion de fonction en troisième
Présentation du problème
L’activité a été proposée à des élèves de troisième en introduction au chapitre Notion de fonction.
Une feuille de papier de format A4 a été distribuée à chaque élève.
Deux questions ont été écrites au tableau :
- À partir de cette feuille, comment construit-on le patron d’une boîte sans couvercle ayant la forme d’un pavé droit ?
- Existe t-il un format de boîte ayant un volume maximal ?
La première phase d’approche du problème a été expérimentale : les élèves ont réfléchi dans un premier temps à la forme que devait prendre le patron pour obtenir la boîte sans couvercle.
L’idée d’enlever des carrés à chaque coin de la feuille de départ n’est pas venue tout de suite. Pour la plupart, il leur a fallu manipuler un modèle déjà réalisé pour percevoir la forme du patron.
Ensuite, le débat a été orienté sur la hauteur à prendre pour la boîte : certains avaient bien compris que la hauteur choisie conditionnait la taille du fond de la boîte. Il en est ressorti des contraintes sur le
choix de la hauteur : "entre 0,5 cm et 10 cm" (les élèves ont déterminé ces contraintes pour que la boîte soit réalisable d’un point de vue pratique).
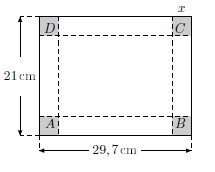
Découpage de la feuille A4
Réalisation de la boîte et calcul de volume
Nous sommes ensuite passés à la phase de réalisation de la boîte : les élèves se sont répartis les différentes hauteurs (certains ont tout de même choisi des hauteurs identiques) et sont passés au tracé du patron, ce qui a permis de retravailler la géométrie de base. Pendant ce temps de réalisation, certaines réflexions ont été émises, notamment plusieurs élèves qui prédisaient que tout le monde obtiendrait le même volume. Le patron étant réalisé, les élèves ont effectué le calcul de volume, ce qui a été l’occasion de revenir sur la formule de volume d’un pavé et sur les unités de volume.
Un relevé de valeurs a été réalisé au tableau et les élèves ont pu se rendre compte des variations du volume : on a ainsi pu établir que le volume de la boîte variait en fonction de la taille du carré découpé.
Modélisation
Après un temps de mise en commun où il a été établi que le volume dépendait de la taille du carré enlevé aux quatre coins, une fiche a été distribuée pour amorcer la modélisation du problème. Cette phase délicate s’est déroulée avec l’appui du professeur : en effet, les élèves ont une certaine appréhension de la "formule" et beaucoup ont correctement exprimé les dimensions de la boîte en fonction de x mais n’osaient pas passer au calcul du volume car "cela ne donnait
rien" (pas de valeur numérique au bout du calcul).
Un retour au calcul littéral, en rappelant le concept de formule, a permis de conclure et d’obtenir l’expression V(x) du volume.
Page suivante : représentation graphique, le recours aux TICE

