Algorithmique et racine carrée en seconde, compléments publié le 03/03/2020  - mis à jour le 20/09/2023

Un peu de nostalgie : l’algorithme de la potence

L’algorithme de la potence, qui tient son nom de la disposition des calculs organisée autour d’une potence comme une division, est un algorithme qui était utilisé jusqu’au milieu du vingtième siècle pour extraire des racines carrées à la main.

Le principe est le suivant : on sépare les chiffres du nombre par paires en commençant à partir de la virgule. On place le nombre dont on veut extraire la racine en haut, de la même façon que lorsqu’on effectue une division selon la méthode classique ; la racine carrée sera inscrite à la place réservée normalement au diviseur dans une division posée classique.
On commence par abaisser la première tranche $t_0$ et on cherche le plus grand nombre $x$ tel que $x^2\leqslant t_0$. Ce nombre $x$ est le premier chiffre de la racine (à partir de la gauche) et on le note $r$. On soustrait ensuite $x^2$ à $t_0$ de sorte que l’on ait un premier reste.
À chaque étape :

• on abaisse la paire de chiffres suivante et on la place au côté d’un reste éventuel de l’étape précédente (initialement nul) ;
• soit $r$ le résultat intermédiaire de la racine carrée obtenu précédemment (égal à zéro au début). On cherche le plus grand chiffre $x$ tel que le nombre $y=(20r + x)x$ ne dépasse pas le reste courant ;
• on complète $r$ en plaçant la décimale $x$ à sa droite, pour former le nouveau résultat intermédiaire ;
• on soustrait $y$ de la valeur courante pour former le nouveau reste ;
• si le reste est nul et qu’il n’y a plus de chiffre à abaisser alors l’algorithme se termine sinon on recommence.

Exemple : Extraction de $\sqrt{238}$ au millième

• étape 1 : écrire le nombre dont on veut extraire la racine comme le dividende d’une division.
• étape 2 : séparer en tranches de deux chiffres à partir de la droite ; la dernière tranche à gauche peut
  n’avoir qu’un chiffre
• étape 3 : extraire la racine carrée de la première tranche, c’est-à-dire trouver le plus grand nombre $x$ tel que $x^2\leqslant 2$. Ici c’est 1. L’écrire au diviseur.
• étape 4 : soustraire le carré de ce nombre à la tranche et abaisser la tranche suivante. On a 138
• étape 5 : prendre le double du chiffre du diviseur,
• étape 6 : chercher le chiffre qui donne le produit le plus proche, en restant inférieur
  au nombre abaissé : par exemple ici on doit faire $2\ldots \times \ldots\leqslant 138$, on essaie avec $21\times 1$, $22\times 2$, $23\times 3$,... et on obtient $25\times 5=125$. Le deuxième chiffre de la racine est 5
• étape 7 : écrire le chiffre obtenu au diviseur et soustraire le produit obtenu, 125, au nombre abaissé
• étape 8 : abaisser la tranche suivante : si on est au bout du nombre entier et que l’on veut poursuivre l’extraction,
  on abaisse une paire de zéros et on met une virgule au diviseur.
• étape 9 et 10 : poursuivre le processus jusqu’à la précision demandée, chaque tranche de deux chiffres abaissée produisant un chiffre supplémentaire dans l’écriture de la racine .

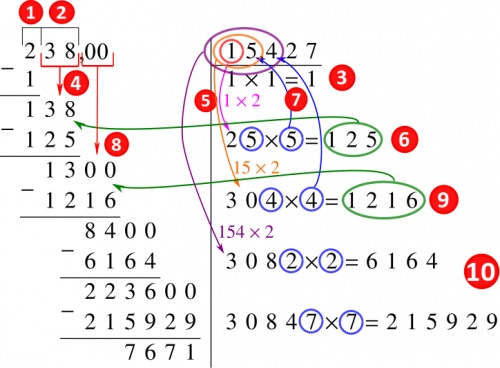
Cette figure illustre le fonctionnement de l’algorithme de la potence utilisé pour extraire des racines carrées à la main

Pour des exemples de mise en œuvre et une justification théorique de la méthode, vous pouvez visualiser la vidéo de la chaîne YouTube Hans Samble - Maths au lycée, qui propose par ailleurs de très nombreuses vidéos mathématiques de qualité :

L’implémentation en Python s’appuie sur les chaînes de caractères, un nombre entier pouvant être converti en une chaine de caractères qui sera ensuite découpée en tranches de longueur 2. Le programme ci-dessous s’applique à des entiers car l’algorithme de la potence ne tient pas compte de la virgule : un nombre décimal est considéré sans sa virgule et celle-ci peut être indiquée dans la racine mais non prise en compte dans le processus de calcul.

Il faut au préalable construire une fonction de tranchage qui tronçonne la chaine formée par le nombre en chaînes de deux chiffres (voir exécution en ligne) :

l’appel de cette fonction donne une liste de chaînes de deux caractères, sauf éventuellement pour la dernière :

Cette fonction est ensuite utilisée pour mettre en œuvre l’algorithme de la potence (voir exécution en ligne) :

L’appel de la fonction donne :

Si l’on veut la racine carrée d’un nombre décimal, on le transforme en entier en le décalant d’un nombre pair de rangs $n=2p$ vers la droite et on calcule cet entier à la précision souhaitée puis on récupère la racine carrée du nombre décimal en décalant de $p$ rang(s) vers la gauche :