
Un nouveau modèle : la fonction exponentielle publié le 08/03/2020 - mis à jour le 09/04/2021
Sommaire des TraAms "modéliser"
Description de la tâche de modélisation
Problématique
La fonction exponentielle est intimement liée à la notion de la loi de refroidissement. Les élèves s’approprient cette nouvelle fonction au travers d’une expérience de refroidissement de l’eau.
Niveau concerné
Classe de Première Spécialité (expérimentation menée avec une terminale S)
Modèle(s) mathématiques utilisé(s)
Fonction exponentielle/ Équation différentielle
Autres compétences mathématiques mises en jeu
Calculer : résolution d’équations à l’aide de Geogebra/Représenter : changer de cadre (tableau de valeurs, représentation graphique)
Compétences numériques
Création de contenu/Communication&Collaboration
Nombre d’heures envisagées
Une séance d’une heure
Démarche de l’enseignant
La fonction exponentielle est présente dans de nombreux domaines mais la compréhension de son utilité peut parfois s’avérer bien compliqué. Le programme de Mathématiques est dense et il est souvent difficile d’allier le sens et la technicité.
La loi de refroidissement illustre parfaitement l’intérêt des Mathématiques dans la vie réelle. Elle permet de prévoir l’évolution de la température au cours du temps. Elle s’illustre parfaitement dans la datation des cadavres.
Il s’agit donc dans cette expérimentation de présenter cette nouvelle fonction au travers de mesures de températures en fonction du temps.
Description du déroulement de la séance
En amont de la séance, les élèves ont répondu à ce questionnaire au format Googleforms.
Ce questionnaire permet aux élèves de s’approprier les notions d’équations différentielles et l’utilisation du calcul formel de Geogebra pour les résoudre.
Les réponses m’ont permis d’anticiper les difficultés des élèves. Ils semblaient avoir globalement bien compris la notion d’équations différentielles. Les résultats en témoignent :
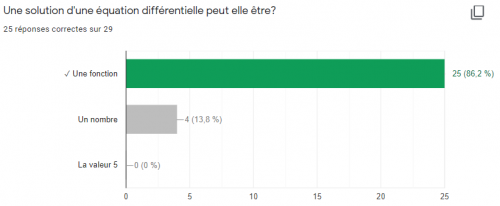
Les résultats des élèves à la question :
Une solution d’une équation différentielle peut elle être ?
J’ai donc introduit la séance par une mise en scène sur mon expérience réalisée à la maison à l’aide du diaporama. Cela a suscité l’intérêt des élèves. J’ai alors proposé le questionnement : Au bout de combien de temps le thé sera-t-il à 40°C ?
Je me suis alors appuyé sur le padlet pour montrer que la loi de refroidissement de Newton amenait à résoudre une équation différentielle. Là encore, la préparation en amont de ce questionnaire m’a permis de lancer rapidement la problématique.
Padlet qui présente les recherches des élèves sur le refroidissement du thé
J’ai alors présenté le relevé et j’ai montré que la variation du temps par rapport à la température est à "peu près" constante. J’ai alors proposé le coefficient suivant -2,4 en réalisant une "moyenne".
Voici les résultats obtenus :
Relevé de valeurs de température et calculs effectués avec le tableur pour obtenir une approximation du coefficient de la loi de refroidissement.
J’ai donc abouti à la relation : T ’ (x)=-2,4 (T ( x)−20,5). Les élèves ont reconnu une équation différentielle. Nous avons échangé sur une possible fonction qui pouvait être solution de cette équation différentielle.
Ils sont ensuite passés sur Geogebra pour résoudre cette équation différentielle.
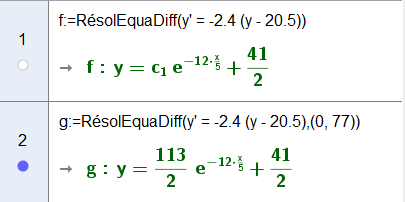
Production élève : résolution de l’équation différentielle avec le calcul formel de Geogebra
J’ai alors fait émerger en synthèse cette nouvelle fonction. Elle vérifie f’(x) = f(x) et f(0) = 1
J’ai choisi de démontrer l’unicité cette fonction avec l’appui d’une vidéo :
Les élèves et la modélisation
Globalement, cette expérimentation soulève le problème du temps. Comment aborder et faire comprendre cette modélisation tout en laissant les élèves travailler le côté technique des propriétés de l’exponentielle ? L’approche anticipée du google forms permet de surmonter une partie de cette difficulté. En effet, les élèves sont déjà avant la séance sensibilisés à la notion d’équation différentielle.
Par ailleurs, la mise en scène autour de la recherche permet d’impliquer les élèves. Ils se sont questionnés sur l’évolution de la température. Le côté ludique de la température du thé permet de contextualiser la situation d’enseignement-apprentissage. La "moyenne" obtenue avec le tableur pour arriver à l’équation différentielle est critiquable mais les élèves ont néanmoins accepté cette approximation sans réactions.
L’utilisation de Geogebra est largement accessible. Chaque élève a pu manipuler les commandes pour atteindre l’apparition de la fonction exponentielle. En revanche, la condition initiale (la température vaut 77°C à l’instant 0) constitue une difficulté supplémentaire mais doit cependant être comprise pour atteindre la forme explicite de la fonction et ainsi prévoir le temps nécessaire pour obtenir une température de 40°C.
La réponse est à tempérer devant les élèves. Elle est à confronter avec le monde réel. On peut alors discuter des conditions dans lesquelles cette expérience a été réalisée. On peut s’interroger sur le moment où nous modélisons : est-ce l’équation différentielle ? Est-ce la fonction exponentielle obtenue ? Est ce tout le cycle de la réflexion ?
Cette séance s’inscrit dans le dispositif classe ouverte de l’académie de Poitiers. Voici les retours des collègues observateurs :
Rapport exposant les ressentis des collègues observateurs dans le cadre de la classe ouverte.
Prolongement et perspectives
Afin que le calcul formel de Geogebra ne constitue pas une difficulté, il semble préférable de les faire travailler en amont autour d’un exercice plus abordable. On pourra alors faire découvrir les commandes pour résoudre des équations, déterminer une dérivée...
Voici un exemple de tâche à proposer aux élèves.
Ce document présente une tâche pour permettre aux élèves de s’approprier plus facilement les commandes du calcul formel de Geogebra avant le travail de cette séance.
L’avantage de s’appuyer sur une vidéo pour démontrer l’unicité permet aux élèves de la reprendre à la maison plus facilement. Il convient ensuite de travailler le côté technique de l’utilisation des propriétés de la fonction exponentielle.
Dans ce cadre, on peut proposer un "parcours fléché".
Voici une proposition :
Ce document sous forme de parcours fléchés propose une découverte des premières propriétés à l’aide de vidéos explicatives.
Documents de référence
Diaporama présentant pour les élèves l’expérience de refroidissement de l’eau pour le thé.
Relevé des valeurs de la température de l’eau en fonction du temps obtenues suite à l’expérience
Document élève sur la loi de refroidissement permettant d’introduire la fonction exponentielle.
Document professeur sur la loi de refroidissement permettant d’introduire la fonction exponentielle

